Advertisements
Advertisements
प्रश्न
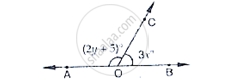
In the below Fig, OA and OB are opposite rays.
If y = 35°, what is the value of x?
उत्तर १
Given that if y = 35°
`∠`AOC + `∠`BOC = 180°
(2 y + 5) + 3x = 180°
(2 (35) + 5) + 3x = 180°
(70 + 5) + 3x = 180°
3x = 180° - 75°
3x = 105°
x = 35°
x = 35°
उत्तर २
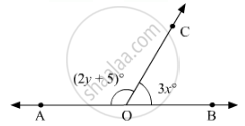
In figure:
Since OA and OB are opposite rays. Therefore, AB is a line. Since, OC stands on line AB.
Thus,∠AOCand ∠BOC form a linear pair, therefore, their sum must be equal to180°.
Or, we can say that
∠AOC + ∠BOC = 180°
From the given figure:
∠AOC= (2y + 5)and ∠BOC = 3x
On substituting these two values, we get
`(2y + 5) + 3x = 180`
`3x + 2y = 180 -5`
3x + 2y = 175 ...(i)
On putting in y =35 in equation (A), we get:
`3x + 2(35) =175`
`3x + 70 = 175`
`3x = 175 - 70`
`3x = 105`
`x = 105/3`
`x = 35`
Hence, the value of x is 35.
APPEARS IN
संबंधित प्रश्न
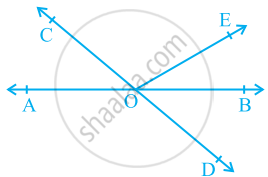
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
Write the supplement of the following angles .
138°
The measure of an angle is twice the measure of its supplementary ang Find its measure.
In the below fig, AOC is a line, find x.
In Fig. 8.42, a is greater than b by one third of a right-angle. Find the values of a and b.
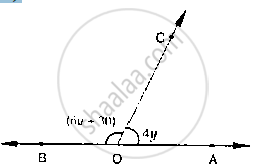
What value of y would make AOB a line in below fig, if ∠AOC = 4y and ∠BOC = (6y +
30)
Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary
In the below fig, `∠`1 = 60° and `∠`2 = `(2/3)^(rd)`of a right angle. Prove that l || m.
The opposite sides of a quadrilateral are parallel. If one angle of the quadrilateral is 60°,
find the other angles.
If two lines intersect, prove that the vertically opposite angles are equal.
