Advertisements
Advertisements
प्रश्न
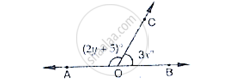
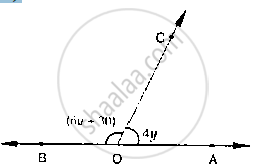
In the below Fig, OA and OB are opposite rays :
If x = 25°, what is the value of y?
उत्तर १
Given that x = 25°
Since `∠`AOC and `∠`BOC form a linear pair
`∠`AOC + `∠`BOC = 180°
Given that
`∠`AOC = 2 y + 5 and `∠`BOC = 3x
∴ `∠`AOC + `∠`BOC = 180°
(2 y + 5)° + 3x = 180°
(2 y + 5)° + 3(25°) = 180°
2 y° + 5° + 75° = 180°
2 y° + 80° = 180°
2 y° = 180° - 80° = 100°
y° = `(100°)/2` = 50°
⇒ y = 50°
उत्तर २
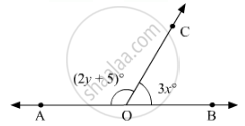
In figure:
Since OA and OB are opposite rays. Therefore, AB is a line. Since, OC stands on line AB.
Thus,∠AOCand ∠BOC form a linear pair, therefore, their sum must be equal to180°.
Or, we can say that
∠AOC + ∠BOC = 180°
From the given figure:
∠AOC= (2y + 5)and ∠BOC = 3x
On substituting these two values, we get
`(2y + 5) + 3x = 180`
`3x + 2y = 180 -5`
3x + 2y = 175 ...(i)
On putting x = 25in (i), we get:
`3(25 )+2y = 175`
`75 + 2y = 175`
`2y = 175 - 75`
`2y = 100`
`y = 100/2`
`y = 50`
Hence, the value of y is 50.
APPEARS IN
संबंधित प्रश्न
If the supplement of an angle is three times its complement, find the angle.
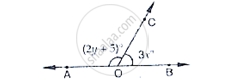
In the below Fig, OA and OB are opposite rays.
If y = 35°, what is the value of x?
In the below fig, AOC is a line, find x.
What value of y would make AOB a line in below fig, if ∠AOC = 4y and ∠BOC = (6y +
30)
If below fig, ∠AOF and ∠FOG form a linear pair.
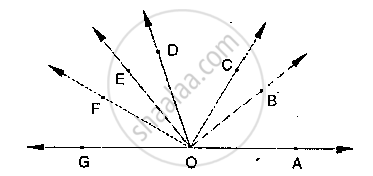
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°
(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
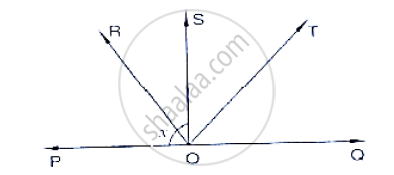
In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS
and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
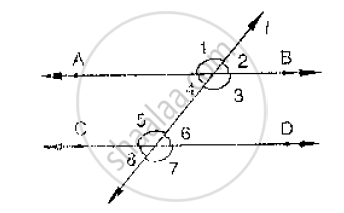
In below fig, AB CD and ∠1 and ∠2 are in the ratio 3 : 2. Determine all angles from 1 to 8.
If below fig, if AB || CD and CD || EF, find ∠ACE.
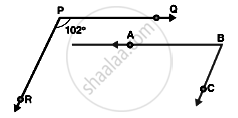
In the below, PQ || AB and PR || BC. If `∠`QPR = 102°, determine `∠`ABC. Give reasons.
In the given figure, if l1 || l2, what is the value of x?

