Advertisements
Advertisements
प्रश्न
If below fig, ∠AOF and ∠FOG form a linear pair.
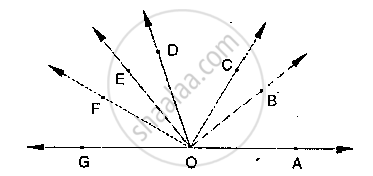
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°
(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
उत्तर
(i) `∠`FOE = x, `∠`DOE = y and `∠`BOC = z sat
Since `∠`AOF , `∠`FOG is Linear pair
⇒`∠`AOF + 30° = 180° [`∠`AOF + `∠`FOG = 180° and `∠`FOG = 30°]
⇒ `∠`AOF = 180° - 30°
⇒ `∠`AOF = 150°
⇒ `∠` AOB + `∠`BOC + `∠`COD + `∠`DOE + `∠`EOF = 150°
⇒ 30° + z + 30° + y + x = 150°
⇒ x + y + z = 150° - 30° - 30°
⇒ x + y + z = 90° .....(1)
Now `∠`FOC = 90°
⇒ `∠`FOE + `∠`EOD + `∠`DOC = 90°
⇒ x + y + 30° = 90°
⇒ x + y = 90° - 30°
⇒ x + y = 60° .....(2)
Substituting (2) in (1)
x + y + z = 90°
⇒ 60 + z = 90° Þ z = 90° - 60° = 30°
i.e., `∠`BOC = 30°
Given `∠`BOE = 90°
⇒`∠`BOC + `∠`COD + `∠`DOE = 90°
⇒ 30° + 30° + `∠`DOE = 90°
⇒ `∠`DOE = 90° - 60° = 30°
∴ `∠`DOE = x = 30°
Now, also we have
x + y = 60°
⇒ y = 60° - x = 60° - 30° = 30°
`∠`FOE = 30
(ii) Right angles are
`∠`DOG, `∠`COF , `∠`BOF , `∠`AOD
(iii) Three pairs of adjacent complementary angles are
`∠`AOB, `∠`BOD;
`∠`AOC, `∠`COD;
`∠`BOC, `∠`COE
(iv) Three pairs of adjacent supplementary angles are
`∠`AOB, `∠`BOG;
`∠`AOC, `∠`COG;
`∠`AOD, `∠`DOG.
(v) Three pairs of adjacent angles
`∠`BOC, `∠`COD;
`∠`COD, `∠`DOE;
`∠`DOE, `∠`EOF ,
APPEARS IN
संबंधित प्रश्न
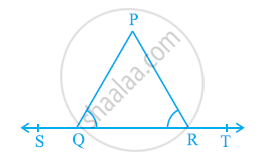
In the given figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
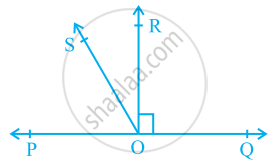
In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = `1/2` (∠QOS − ∠POS).
Write the complement of the following angles .
35°
Two supplementary angles differ by 48°. Find the angles.
An angle is 14° more than its complementary angle. What is its measure?
In the below Fig, OA and OB are opposite rays.
If y = 35°, what is the value of x?
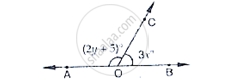
In the below Fig, ∠AOC and ∠BOC form a linear pair. if a − 2b = 30°, find a and b.
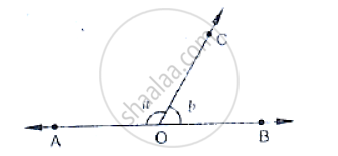
Given ∠POR = 3x and ∠QOR = 2x + 10, find the value of x for which POQ will be a line.
(Below fig).
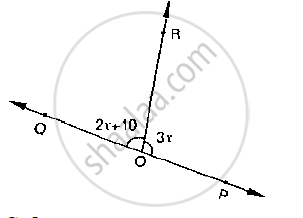
In the below fig, if l || m, n || p and ∠1 = 85°, find `∠`2.
Two unequal angles of a parallelogram are in the ratio 2 : 3. Find all its angles in degrees .
