Advertisements
Advertisements
प्रश्न
If below fig, ∠AOF and ∠FOG form a linear pair.
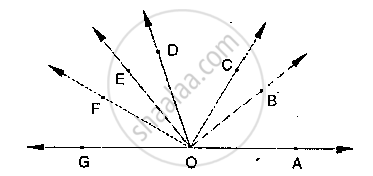
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°
(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
उत्तर
(i) `∠`FOE = x, `∠`DOE = y and `∠`BOC = z sat
Since `∠`AOF , `∠`FOG is Linear pair
⇒`∠`AOF + 30° = 180° [`∠`AOF + `∠`FOG = 180° and `∠`FOG = 30°]
⇒ `∠`AOF = 180° - 30°
⇒ `∠`AOF = 150°
⇒ `∠` AOB + `∠`BOC + `∠`COD + `∠`DOE + `∠`EOF = 150°
⇒ 30° + z + 30° + y + x = 150°
⇒ x + y + z = 150° - 30° - 30°
⇒ x + y + z = 90° .....(1)
Now `∠`FOC = 90°
⇒ `∠`FOE + `∠`EOD + `∠`DOC = 90°
⇒ x + y + 30° = 90°
⇒ x + y = 90° - 30°
⇒ x + y = 60° .....(2)
Substituting (2) in (1)
x + y + z = 90°
⇒ 60 + z = 90° Þ z = 90° - 60° = 30°
i.e., `∠`BOC = 30°
Given `∠`BOE = 90°
⇒`∠`BOC + `∠`COD + `∠`DOE = 90°
⇒ 30° + 30° + `∠`DOE = 90°
⇒ `∠`DOE = 90° - 60° = 30°
∴ `∠`DOE = x = 30°
Now, also we have
x + y = 60°
⇒ y = 60° - x = 60° - 30° = 30°
`∠`FOE = 30
(ii) Right angles are
`∠`DOG, `∠`COF , `∠`BOF , `∠`AOD
(iii) Three pairs of adjacent complementary angles are
`∠`AOB, `∠`BOD;
`∠`AOC, `∠`COD;
`∠`BOC, `∠`COE
(iv) Three pairs of adjacent supplementary angles are
`∠`AOB, `∠`BOG;
`∠`AOC, `∠`COG;
`∠`AOD, `∠`DOG.
(v) Three pairs of adjacent angles
`∠`BOC, `∠`COD;
`∠`COD, `∠`DOE;
`∠`DOE, `∠`EOF ,
APPEARS IN
संबंधित प्रश्न
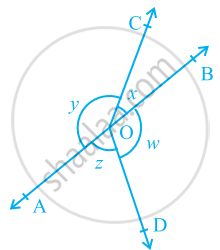
In the given figure, if x + y = w + z, then prove that AOB is a line.
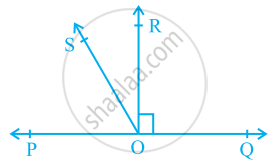
In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = `1/2` (∠QOS − ∠POS).
Write the complement of the following angles .
35°
Write the supplement of the following angles .
54°
Write the supplement of the following angles .
138°
An angle is equal to 8 times its complement. Determine its measure.
If the complement of an angle is equal to the supplement of the thrice of it. Find the measure of the angle.
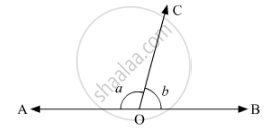
In Fig. 8.42, a is greater than b by one third of a right-angle. Find the values of a and b.
Two unequal angles of a parallelogram are in the ratio 2 : 3. Find all its angles in degrees .
In the given figure, if AB || HF and DE || FG, then the measure of ∠FDE is