Advertisements
Advertisements
प्रश्न
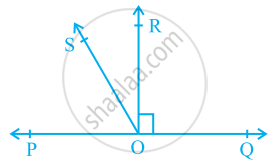
In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = `1/2` (∠QOS − ∠POS).
उत्तर
It is given that OR ⊥ PQ
∴ ∠POR = 90°
⇒ ∠POS + ∠SOR = 90°
∠ROS = 90° − ∠POS …(1)
∠QOR = 90° ...(As OR ⊥ PQ)
∠QOS − ∠ROS = 90°
∠ROS = ∠QOS − 90° …(2)
On adding equations (1) and (2), we obtain
2 ∠ROS = ∠QOS − ∠POS
∴ ∠ROS = `1/2` (∠QOS − ∠POS)
APPEARS IN
संबंधित प्रश्न
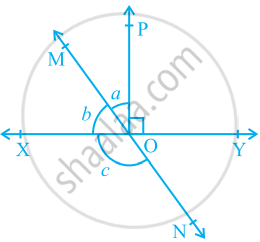
In the given figure, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
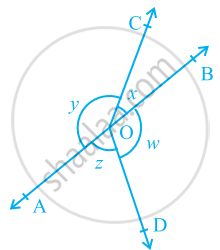
In the given figure, if x + y = w + z, then prove that AOB is a line.
Two supplementary angles differ by 48°. Find the angles.
If the angles (2x −10)° and (x − 5)° are complementary angles, find x.
If the supplement of an angle is two-third of itself. Determine the angle and its supplement.
In the below Fig, OA and OB are opposite rays.
If y = 35°, what is the value of x?
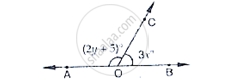
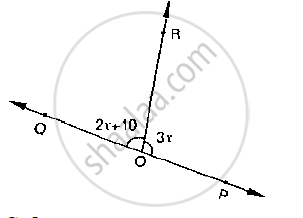
Given ∠POR = 3x and ∠QOR = 2x + 10, find the value of x for which POQ will be a line.
(Below fig).
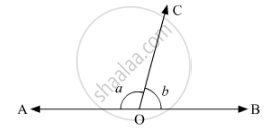
In Fig. 8.42, a is greater than b by one third of a right-angle. Find the values of a and b.
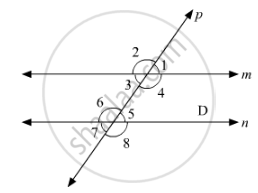
In the below fig, transversal 𝑙 intersects two lines m and n, `∠`4 = 110° and `∠`7 = 65°. Is m || n?
Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then each pair of corresponding
angles are _______
