Advertisements
Advertisements
प्रश्न
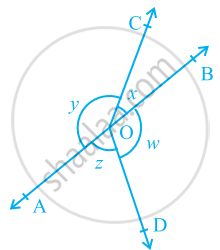
In the given figure, if x + y = w + z, then prove that AOB is a line.
उत्तर
Given: x + y = w + z
To prove: AOB is a straight line.
Proof: x + y + w + z = 360°
or x + y + x + y = 360°
⇒ 2x + 2y = 360°
⇒ 2(x + y) = 360°
⇒ x + y = 180° ...(Linear pair)
When the sum of two adjacent angles is 180°, then the line is straight and straight.
Hence, AOB is a line.
APPEARS IN
संबंधित प्रश्न
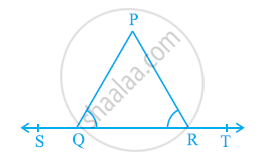
In the given figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
Write the complement of the following angles.
77°
Write the supplement of the following angles .
54°
Write the supplement of the following angles.
132°
If an angle differs from its complement by 10°, find the angle .
In the below Fig, OA and OB are opposite rays :
If x = 25°, what is the value of y?
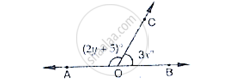
In Fig. 8.42, a is greater than b by one third of a right-angle. Find the values of a and b.
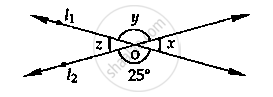
In the given fig, find the values of x, y and z.
The opposite sides of a quadrilateral are parallel. If one angle of the quadrilateral is 60°,
find the other angles.
In the below fig, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of
∠DEF. Prove that ∠ABC + ∠DEF = 180°.