Advertisements
Advertisements
प्रश्न
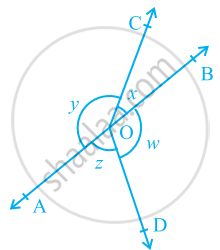
In the given figure, if x + y = w + z, then prove that AOB is a line.
उत्तर
Given: x + y = w + z
To prove: AOB is a straight line.
Proof: x + y + w + z = 360°
or x + y + x + y = 360°
⇒ 2x + 2y = 360°
⇒ 2(x + y) = 360°
⇒ x + y = 180° ...(Linear pair)
When the sum of two adjacent angles is 180°, then the line is straight and straight.
Hence, AOB is a line.
APPEARS IN
संबंधित प्रश्न
Write the complement of the following angle.
20°
Write the complement of the following angles .
35°
An angle is equal to 8 times its complement. Determine its measure.
If an angle differs from its complement by 10°, find the angle .
If the supplement of an angle is two-third of itself. Determine the angle and its supplement.
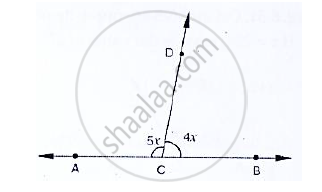
In the below fig, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.
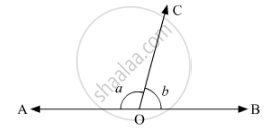
In Fig. 8.42, a is greater than b by one third of a right-angle. Find the values of a and b.
statement are true and false
Angles forming a linear pair can both the acute angles.
Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then each pair of corresponding
angles are _______
In the given figure, if l1 || l2, what is the value of x?

