Advertisements
Advertisements
Question
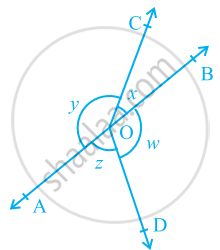
In the given figure, if x + y = w + z, then prove that AOB is a line.
Solution
Given: x + y = w + z
To prove: AOB is a straight line.
Proof: x + y + w + z = 360°
or x + y + x + y = 360°
⇒ 2x + 2y = 360°
⇒ 2(x + y) = 360°
⇒ x + y = 180° ...(Linear pair)
When the sum of two adjacent angles is 180°, then the line is straight and straight.
Hence, AOB is a line.
APPEARS IN
RELATED QUESTIONS
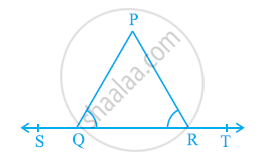
In the given figure, ∠PQR = ∠PRQ, then prove that ∠PQS = ∠PRT.
Write the complement of the following angles .
35°
Write the supplement of the following angles .
138°
If an angle differs from its complement by 10°, find the angle .
If the supplement of an angle is two-third of itself. Determine the angle and its supplement.
In the below fig, write all pairs of adjacent angles and all the linear pairs .

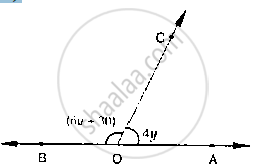
What value of y would make AOB a line in below fig, if ∠AOC = 4y and ∠BOC = (6y +
30)
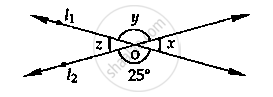
In the given fig, find the values of x, y and z.
AB, CD and EF are three concurrent lines passing through the point O such that OF bisects
∠BOD. If ∠BOF = 35°, find ∠BOC and ∠AOD.
If two lines intersect, prove that the vertically opposite angles are equal.
