Advertisements
Advertisements
Question
If two lines intersect, prove that the vertically opposite angles are equal.
Solution
Let us draw the figure.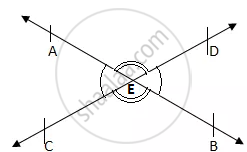
Here, we can see that
AB and CD intersect each other at point E.
The two pairs of vertically opposite angles are:
1st pair – ∠AEC and ∠BED
2nd pair – ∠AED and ∠BEC
We need to prove that the vertically opposite angles are equal, i.e.,
∠AEC = ∠BED and ∠AED = ∠BEC
Now, we can see that the ray AE stands on the line CD.
We know, if a ray stands on a line then the sum of the adjacent angles is equal to 180°.
⇒ ∠AEC + ∠AED = 180° (By linear pair axiom) ...(i)
Similarly, the ray DE stands on the line AEB.
⇒ ∠AED + ∠BED = 180° (By linear pair axiom) ...(ii)
From equations (i) and (ii), we have
∠AEC + ∠AED = ∠AED + ∠BED
⇒ ∠AEC = ∠BED ...(iii)
Similarly, the ray BE stands on the line CED.
⇒ ∠DEB + ∠CEB = 180° (By linear pair axiom) ...(iv)
Also, the ray CE stands on the line AEB.
⇒ ∠CEB + ∠AEC = 180° (By linear pair axiom) ...(v)
From equations (iv) and (v), we have
∠DEB + ∠CEB = ∠CEB + ∠AEC
⇒ ∠DEB = ∠AEC ...(vi)
Thus, from equation (iii) and equation (vi), we have
∠AEC = ∠BED and ∠DEB = ∠AEC
Therefore, it is proved that the vertically opposite angles are equal.
APPEARS IN
RELATED QUESTIONS
Write the complement of the following angles.
90°
Two supplementary angles differ by 48°. Find the angles.
If the supplement of an angle is three times its complement, find the angle.
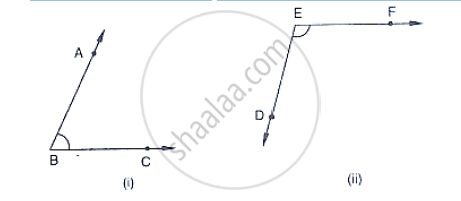
In the below fig, write all pairs of adjacent angles and all the linear pairs .

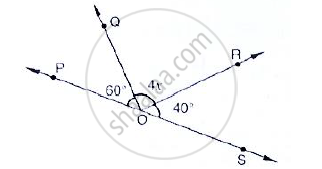
In the below fig, POS is a line, find x.
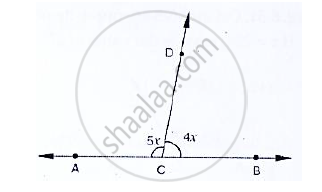
In the below fig, ACB is a line such that ∠DCA = 5x and ∠DCB = 4x. Find the value of x.
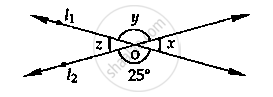
In the given fig, find the values of x, y and z.
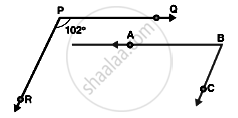
In the below, PQ || AB and PR || BC. If `∠`QPR = 102°, determine `∠`ABC. Give reasons.
Two unequal angles of a parallelogram are in the ratio 2 : 3. Find all its angles in degrees .
In the below fig, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of
∠DEF. Prove that ∠ABC + ∠DEF = 180°.