Advertisements
Advertisements
Question
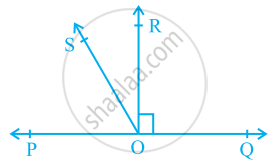
In the given figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS = `1/2` (∠QOS − ∠POS).
Solution
It is given that OR ⊥ PQ
∴ ∠POR = 90°
⇒ ∠POS + ∠SOR = 90°
∠ROS = 90° − ∠POS …(1)
∠QOR = 90° ...(As OR ⊥ PQ)
∠QOS − ∠ROS = 90°
∠ROS = ∠QOS − 90° …(2)
On adding equations (1) and (2), we obtain
2 ∠ROS = ∠QOS − ∠POS
∴ ∠ROS = `1/2` (∠QOS − ∠POS)
APPEARS IN
RELATED QUESTIONS
Write the supplement of the following angles.
132°
Two supplementary angles are in the ratio 4 : 5. Find the angles.
An angle is 14° more than its complementary angle. What is its measure?
The measure of an angle is twice the measure of its supplementary ang Find its measure.
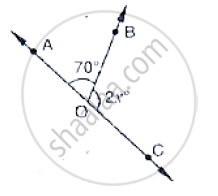
In the below Fig, OA and OB are opposite rays :
If x = 25°, what is the value of y?
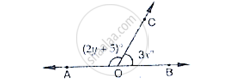
In the below fig, AOC is a line, find x.
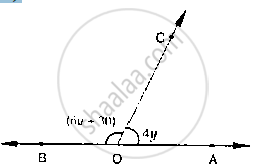
What value of y would make AOB a line in below fig, if ∠AOC = 4y and ∠BOC = (6y +
30)
In below figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD =
40°, find ∠BOE and reflex ∠COE.
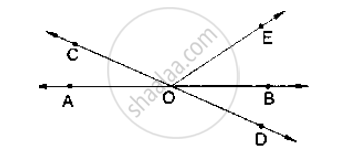
AB, CD and EF are three concurrent lines passing through the point O such that OF bisects
∠BOD. If ∠BOF = 35°, find ∠BOC and ∠AOD.
In the below fig, transversal 𝑙 intersects two lines m and n, `∠`4 = 110° and `∠`7 = 65°. Is m || n?