Advertisements
Advertisements
Question
In the below fig, transversal 𝑙 intersects two lines m and n, `∠`4 = 110° and `∠`7 = 65°. Is m || n?
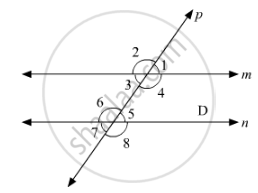
Solution 1
Given:
`∠`4 = 110°, `∠`7 = 65°
To find: Is m || n
Here, `∠`7 =`∠`5= 65° [Vertically opposite angle]
Now,
`∠`4 + `∠`5 = 110 + 65° = 175°
∴m is not parallel to n as the pair of co-interior angles is not supplementary.
Solution 2
The figure is given as follows:
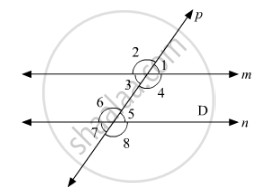
It is given that l is a transversal to lines m and n. Also,
∠4 = 110° and ∠7 = 65°.
We need check whether m||n or not.
We have.∠7 = 65°.
Also,∠7 5.and ∠5are vertically opposite angles, thus, these two must be equal. That is,
∠5 = °65.
Also, ∠4 =110°
Adding this equation to (i), we get:
∠4 + ∠5 =110° +65°
∠4 +∠5 =175°
But these are the consecutive interior angles which are not supplementary.
Theorem states: If a transversal intersects two lines in such a way that a pair of consecutive interior angles is supplementary, then the two lines are parallel.
Thus, m is not parallel to n.
APPEARS IN
RELATED QUESTIONS
Write the complement of the following angle.
20°
Write the complement of the following angles .
35°
If an angle differs from its complement by 10°, find the angle .
The measure of an angle is twice the measure of its supplementary ang Find its measure.
In the given below Fig, find x. Further find ∠BOC, ∠COD and ∠AOD .
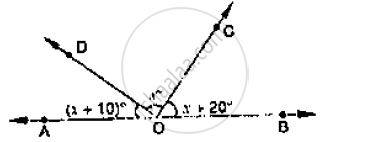
In the below fig, find the value of x.

statement are true and false
Angles forming a linear pair are supplementary.
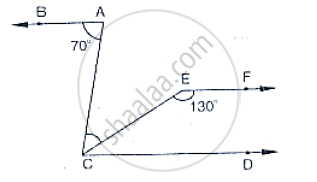
If below fig, if AB || CD and CD || EF, find ∠ACE.
In the below fig, `∠`1 = 60° and `∠`2 = `(2/3)^(rd)`of a right angle. Prove that l || m.
In the given figure, if l1 || l2, what is the value of x?

