Advertisements
Advertisements
Question
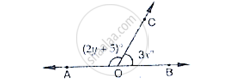
In the below Fig, OA and OB are opposite rays :
If x = 25°, what is the value of y?
Solution 1
Given that x = 25°
Since `∠`AOC and `∠`BOC form a linear pair
`∠`AOC + `∠`BOC = 180°
Given that
`∠`AOC = 2 y + 5 and `∠`BOC = 3x
∴ `∠`AOC + `∠`BOC = 180°
(2 y + 5)° + 3x = 180°
(2 y + 5)° + 3(25°) = 180°
2 y° + 5° + 75° = 180°
2 y° + 80° = 180°
2 y° = 180° - 80° = 100°
y° = `(100°)/2` = 50°
⇒ y = 50°
Solution 2
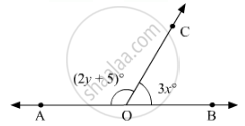
In figure:
Since OA and OB are opposite rays. Therefore, AB is a line. Since, OC stands on line AB.
Thus,∠AOCand ∠BOC form a linear pair, therefore, their sum must be equal to180°.
Or, we can say that
∠AOC + ∠BOC = 180°
From the given figure:
∠AOC= (2y + 5)and ∠BOC = 3x
On substituting these two values, we get
`(2y + 5) + 3x = 180`
`3x + 2y = 180 -5`
3x + 2y = 175 ...(i)
On putting x = 25in (i), we get:
`3(25 )+2y = 175`
`75 + 2y = 175`
`2y = 175 - 75`
`2y = 100`
`y = 100/2`
`y = 50`
Hence, the value of y is 50.
APPEARS IN
RELATED QUESTIONS
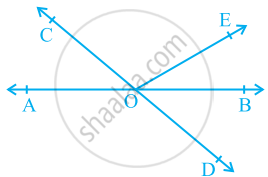
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
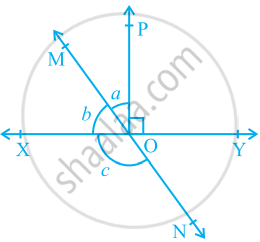
In the given figure, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
How many pairs of adjacent angles, in all, can you name in below fig.?
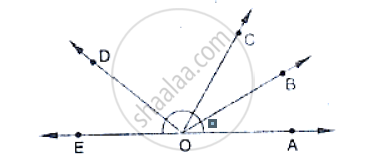
In the below fig, AOC is a line, find x.
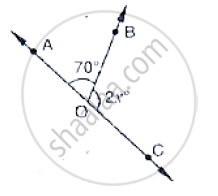
In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS
and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
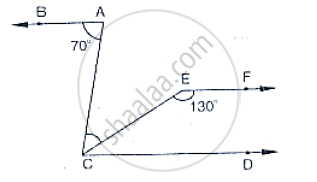
If below fig, if AB || CD and CD || EF, find ∠ACE.
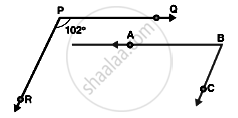
In the below, PQ || AB and PR || BC. If `∠`QPR = 102°, determine `∠`ABC. Give reasons.
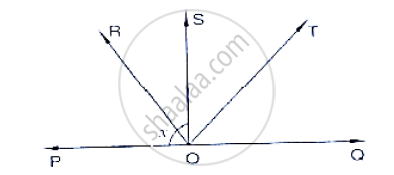
Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary
In the below fig, `∠`1 = 60° and `∠`2 = `(2/3)^(rd)`of a right angle. Prove that l || m.
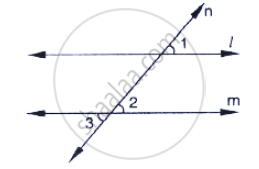
If two lines intersect, prove that the vertically opposite angles are equal.
