Advertisements
Advertisements
Question
Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary
Solution
Consider be angles AOB and ACB

Given OA ⊥ AC, OB ⊥ BC
To prove: `∠`AOB = `∠`ACB (or)
`∠`AOB + `∠`ACB = 180°
Proof:- In a quadrilateral [Sum of angles of quadrilateral]
⇒`∠`A + `∠`O + `∠`B + `∠`C = 360°
⇒ 180 + `∠`O + `∠`C = 360°
⇒ `∠`O + `∠`C = 360 -180 = 180°
Hence, `∠`AOB + `∠`ACB = 180° ......(i )
Also,
`∠`B + `∠`ACB = 180° ......(i )
Also,
`∠`B + `∠`ACB = 180° ......(i )
Also,
`∠`B + `∠`ACB = 180°
⇒ `∠`ACB = 180° - 90°
⇒`∠`ACB = 90° .....(ii)
From (i) and (ii)
∴`∠`ACB = `∠`AOB = 90°
Hence, the angles are equal as well as supplementary
APPEARS IN
RELATED QUESTIONS
Write the complement of the following angles .
30°
Write the supplement of the following angles .
54°
Write the supplement of the following angles .
138°
An angle is 14° more than its complementary angle. What is its measure?
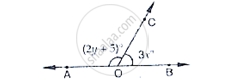
In the below Fig, OA and OB are opposite rays.
If y = 35°, what is the value of x?
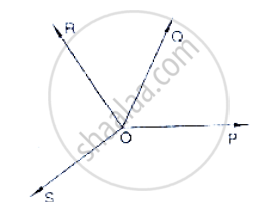
In below fig, OP, OQ, OR and OS arc four rays. Prove that:
∠POQ + ∠QOR + ∠SOR + ∠POS = 360°
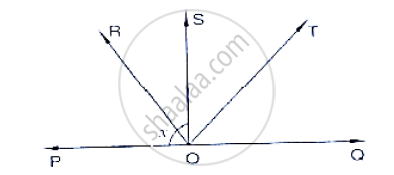
In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS
and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
statement are true and false
Angles forming a linear pair are supplementary.
The opposite sides of a quadrilateral are parallel. If one angle of the quadrilateral is 60°,
find the other angles.
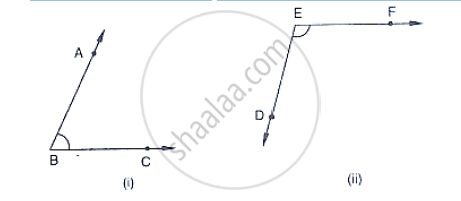
In the below fig, arms BA and BC of ∠ABC are respectively parallel to arms ED and EF of
∠DEF. Prove that ∠ABC + ∠DEF = 180°.