Advertisements
Advertisements
Question
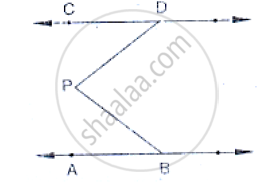
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
Solution
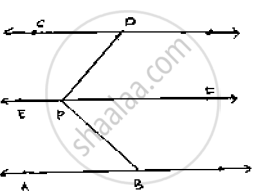
Given that AB || CD
Let EF be the parallel line to AB and CD which passes through P.
It can be seen from the figure
Alternative angles are equal
`∠`ABP = `∠`BPF
Alternative angles are equal
`∠`CDP = `∠`DPF
⇒ `∠`ABP + `∠`CDP = `∠`BPF + `∠`DPF
⇒ `∠`ABP + `∠`CDP = `∠`DPB
Hence proved
AB parallel to CD, P is any point
To prove: `∠`ABP + `∠`BPD + `∠`CDP = 360°
Construction : Draw EF || AB passing through P
Proof:
Since AB || EF and AB || CD
∴EF || CD [Lines parallel to the same line are parallel to each other]
`∠`ABP + `∠`EPB =180° [Sum of co-interior angles is180° AB || EF and BP is the transversal]
`∠`EPD + `∠`COP =180°
[Sum of co-interior angles is180° EF || CD and DP is transversal] …....(1)
`∠`EPD + `∠`CDP =180°
[Sum of Co-interior angles is 180° EF || CD and DP is the transversal] …(2)
By adding (1) and (2)
`∠`ABP + `∠`EPB + `∠`EPD + `∠`CDP = 180° +180°
`∠`ABP + `∠`EPB + `∠`COP = 360°
APPEARS IN
RELATED QUESTIONS
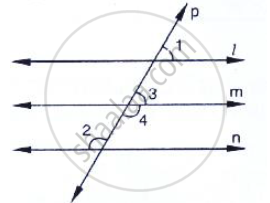
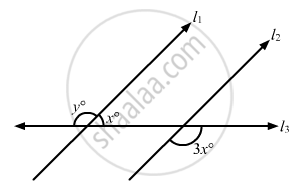
In the below fig, if l || m || n and `∠`1 = 60°, find `∠`2.
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3, then the measure of the larger angle is
In the given figure, if AB || CD, then the value of x is

In the given figure, if l1 || l2, what is x + y in terms of w and z?
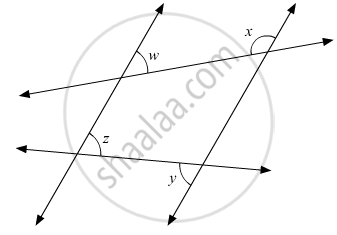
In the given figure, if l1 || l2, what is the value of y?
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
In the following figure, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to ______.

Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
In the following figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.
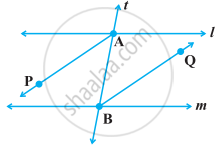
In the following figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF
[Hint: Produce DE to intersect BC at P (say)].