Advertisements
Advertisements
प्रश्न
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
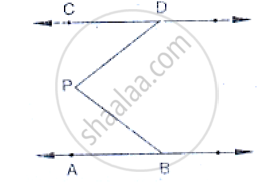
उत्तर
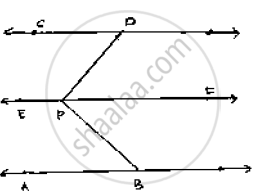
Given that AB || CD
Let EF be the parallel line to AB and CD which passes through P.
It can be seen from the figure
Alternative angles are equal
`∠`ABP = `∠`BPF
Alternative angles are equal
`∠`CDP = `∠`DPF
⇒ `∠`ABP + `∠`CDP = `∠`BPF + `∠`DPF
⇒ `∠`ABP + `∠`CDP = `∠`DPB
Hence proved
AB parallel to CD, P is any point
To prove: `∠`ABP + `∠`BPD + `∠`CDP = 360°
Construction : Draw EF || AB passing through P
Proof:
Since AB || EF and AB || CD
∴EF || CD [Lines parallel to the same line are parallel to each other]
`∠`ABP + `∠`EPB =180° [Sum of co-interior angles is180° AB || EF and BP is the transversal]
`∠`EPD + `∠`COP =180°
[Sum of co-interior angles is180° EF || CD and DP is transversal] …....(1)
`∠`EPD + `∠`CDP =180°
[Sum of Co-interior angles is 180° EF || CD and DP is the transversal] …(2)
By adding (1) and (2)
`∠`ABP + `∠`EPB + `∠`EPD + `∠`CDP = 180° +180°
`∠`ABP + `∠`EPB + `∠`COP = 360°
APPEARS IN
संबंधित प्रश्न
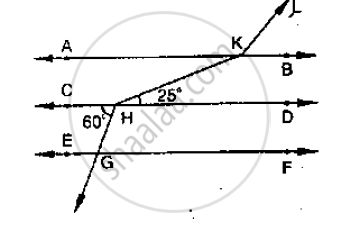
In the below fig, AB || CD || EF and GH || KL. Find `∠`HKL
In the given figure, if AB || CD, then the value of x is

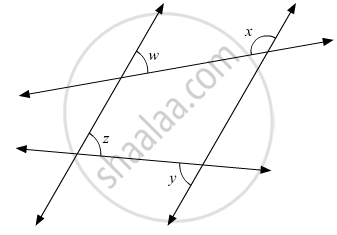
In the given figure, if l1 || l2, what is x + y in terms of w and z?
In the given figure, if AB || CD, then x =

In the given figure, if l || m, then x =

In the following figure, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to ______.

In the following figure, find the value of x for which the lines l and m are parallel.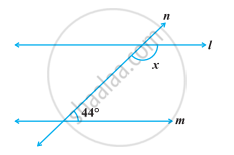
Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
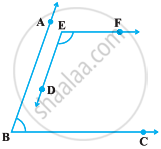
In the following figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°
A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
