Advertisements
Advertisements
प्रश्न
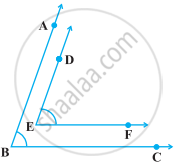
In the following figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°
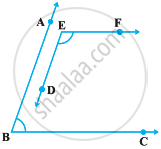
उत्तर
It is given to us:
BA || ED
BC || EF
To show that: ∠ABC + ∠DEF = 180°
Let us extend DE to intersect BC at G and EF to intersect BA at H.
Then, the figure becomes
Since, BA || DE
⇒ BA || GE
We have two parallel lines BA and GE and BG is a transversal intersecting BA and GE at points B and G respectively.
⇒ ∠ABC = ∠EGC ...(i)
Also, BC || EF and GE is a transversal intersecting BC and EF at points G and E respectively.
⇒ ∠EGC = ∠HEG ...(ii)
Since GE is a ray standing on the line HF.
By linear pair axiom,
∠HEG + ∠GEF = 180°
⇒ ∠EGC + ∠GEF = 180° ...[From equation (ii)]
⇒ ∠ABC + ∠GEF = 180°
⇒ ∠ABC + ∠DEF = 180°
Hence, proved.
APPEARS IN
संबंधित प्रश्न
In the below fig, arms BA and BC of `∠`ABC are respectively parallel to arms ED and EF of
`∠`DEF. Prove that `∠`ABC = ∠DEF.
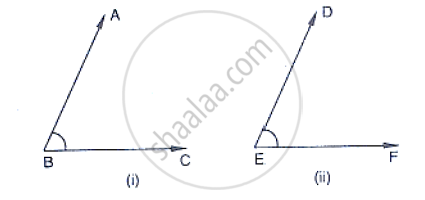
Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
In the given figure, if AB || CD, then the value of x is

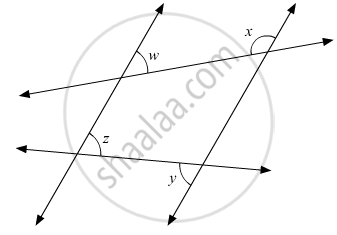
In the given figure, if l1 || l2, what is x + y in terms of w and z?
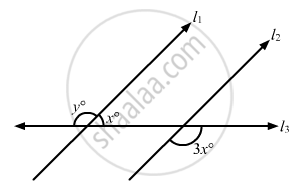
In the given figure, if l1 || l2, what is the value of y?
In the given figure, if l || m, then x =

In the given figure, if \[\frac{y}{x} = 5\] and \[\frac{z}{x} = 4\] then the value of x isc
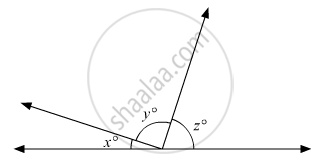
In the given figure, If line segment AB is parallel to the line segment CD, what is the value of y?

In the following figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF
[Hint: Produce DE to intersect BC at P (say)].
A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
