Advertisements
Advertisements
Question
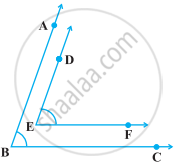
In the following figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°
Solution
It is given to us:
BA || ED
BC || EF
To show that: ∠ABC + ∠DEF = 180°
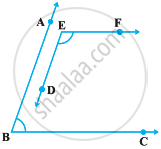
Let us extend DE to intersect BC at G and EF to intersect BA at H.
Then, the figure becomes
Since, BA || DE
⇒ BA || GE
We have two parallel lines BA and GE and BG is a transversal intersecting BA and GE at points B and G respectively.
⇒ ∠ABC = ∠EGC ...(i)
Also, BC || EF and GE is a transversal intersecting BC and EF at points G and E respectively.
⇒ ∠EGC = ∠HEG ...(ii)
Since GE is a ray standing on the line HF.
By linear pair axiom,
∠HEG + ∠GEF = 180°
⇒ ∠EGC + ∠GEF = 180° ...[From equation (ii)]
⇒ ∠ABC + ∠GEF = 180°
⇒ ∠ABC + ∠DEF = 180°
Hence, proved.
APPEARS IN
RELATED QUESTIONS
In the below fig, l, m and n are parallel lines intersected by transversal p at X, Y and Z
respectively. Find ∠1, ∠2 and ∠3.

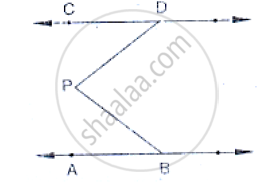
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then interior angles on the same
side of the transversal are _______
Fill in the blank :
If a transversal intersects a pair of lines in such a way that the sum of interior angles
on the same side of transversal is 180°, then the lines are _______.
In the given figure, PQ || RS, ∠AEF = 95°, ∠BHS = 110° and ∠ABC = x°. Then the value of x is

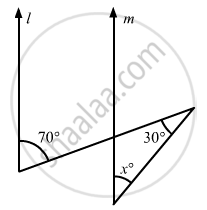
In the given figure, if lines l and m are parallel lines, then x =
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
In the following figure, find the value of x for which the lines l and m are parallel.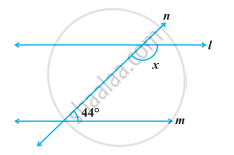
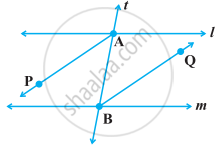
AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (Figure). Show that AP || BQ.
In the following figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF
[Hint: Produce DE to intersect BC at P (say)].