Advertisements
Advertisements
Question
In the given figure, if lines l and m are parallel lines, then x =
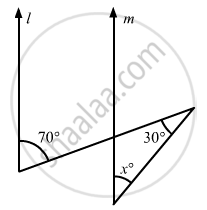
Options
70°
100°
40°
30°
Solution
We have the following figure:
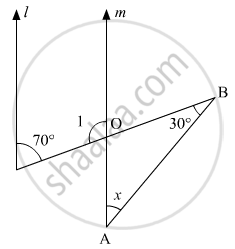
It is given that l || m
We know that consecutive interior angles are supplementary.
Therefore,
∠1 + 70° = 180°
∠1 = 180° - 70°
∠1 = 110° (1)
\[\angle1 = \angle AOB = 110 (\text { vertically opposite angles })\]
In a triangle, we know that, the sum of the angles is supplementary.
In ΔAOB:
\[30^\circ+ x + 110^\circ= 180^\circ\]
\[ \Rightarrow x = 180 - 110 - 30 = 40\]
Hence, the value of x will be \[40^\circ\]
APPEARS IN
RELATED QUESTIONS
In the below fig, if l || m || n and `∠`1 = 60°, find `∠`2.
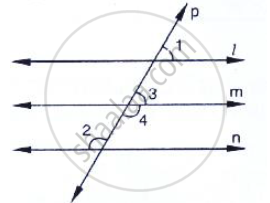
Which pair of lines in the below fig, is parallel? Given reasons.

Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then the interior angles on the same side of the transversal are equal.
If two interior angles on the same side of a transversal intersecting two parallel lines are in the ratio 2:3, then the measure of the larger angle is
In the given figure, if l1 || l2 and l3 || l4, what is y in terms of x?

In the given figure, if l || m, then x =

In the given figure, if lines l and m are parallel, then the value of x is

AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
In the following figure, find the value of x for which the lines l and m are parallel.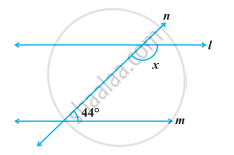
A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
