Advertisements
Advertisements
प्रश्न
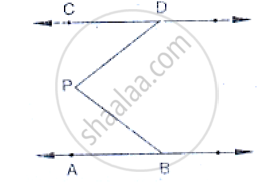
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
उत्तर
Given that AB || CD
Let EF be the parallel line to AB and CD which passes through P.
It can be seen from the figure
Alternative angles are equal
`∠`ABP = `∠`BPF
Alternative angles are equal
`∠`CDP = `∠`DPF
⇒ `∠`ABP + `∠`CDP = `∠`BPF + `∠`DPF
⇒ `∠`ABP + `∠`CDP = `∠`DPB
Hence proved
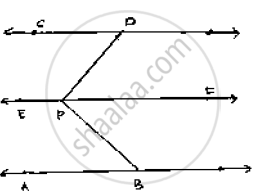
AB parallel to CD, P is any point
To prove: `∠`ABP + `∠`BPD + `∠`CDP = 360°
Construction : Draw EF || AB passing through P
Proof:
Since AB || EF and AB || CD
∴EF || CD [Lines parallel to the same line are parallel to each other]
`∠`ABP + `∠`EPB =180° [Sum of co-interior angles is180° AB || EF and BP is the transversal]
`∠`EPD + `∠`COP =180°
[Sum of co-interior angles is180° EF || CD and DP is transversal] …....(1)
`∠`EPD + `∠`CDP =180°
[Sum of Co-interior angles is 180° EF || CD and DP is the transversal] …(2)
By adding (1) and (2)
`∠`ABP + `∠`EPB + `∠`EPD + `∠`CDP = 180° +180°
`∠`ABP + `∠`EPB + `∠`COP = 360°
APPEARS IN
संबंधित प्रश्न
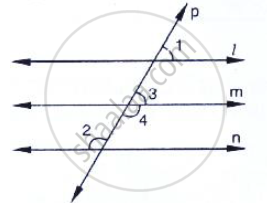
In the below fig, if l || m || n and `∠`1 = 60°, find `∠`2.
Prove that the straight lines perpendicular to the same straight line are parallel to one
another.
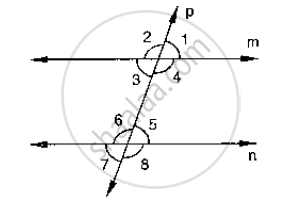
In the below fig, p is a transversal to lines m and n,`∠`2 = 120° and `a∠`5 = 60°. Prove that m || n.
In the below fig, arms BA and BC of `∠`ABC are respectively parallel to arms ED and EF of
`∠`DEF. Prove that `∠`ABC = ∠DEF.
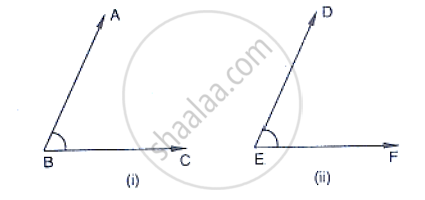
Fill in the blank in the following to make the statement true:
If a transversal intersects a pair of lines in such a way that a pair of alternate angles
are equal, then the lines are _______
In the given figure, if AB || CD, then the value of x is

In the given figure, PQ || RS, ∠AEF = 95°, ∠BHS = 110° and ∠ABC = x°. Then the value of x is

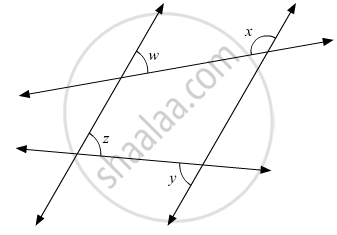
In the given figure, if l1 || l2, what is x + y in terms of w and z?
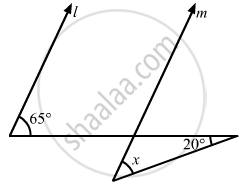
In the given figure, if lines l and m are parallel, then x =
AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
