Advertisements
Advertisements
Question
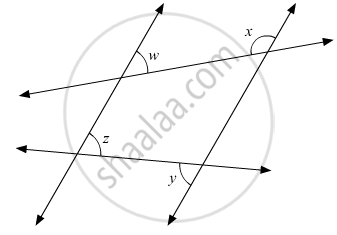
In the given figure, if l1 || l2, what is x + y in terms of w and z?
Options
180° − w + z
180° + w − z
180° - w − z
180° + w + z
Solution
The figure is given below:

Since, y and z are alternate interior opposite angles. Therefore, these must be equal.
y = z (i)
Also x and w are consecutive interior angles.
Theorem states: If a transversal intersects two parallel lines, then each pair of consecutive interior angles are supplementary.
Therefore,
x +w = 180° (ii)
On adding equation (i) and (iii) , we get :
x + y + w = 180°
x + y = 180° + z - w
APPEARS IN
RELATED QUESTIONS
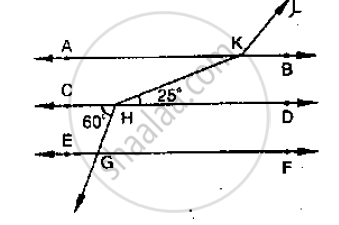
In the below fig, AB || CD || EF and GH || KL. Find `∠`HKL
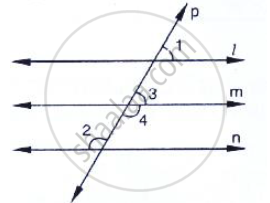
In the below fig, if l || m || n and `∠`1 = 60°, find `∠`2.
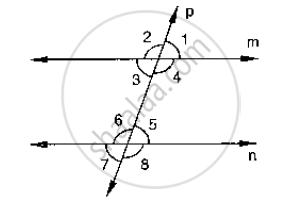
In the below fig, p is a transversal to lines m and n,`∠`2 = 120° and `a∠`5 = 60°. Prove that m || n.
Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
Fill in the blank :
If a transversal intersects a pair of lines in such a way that the sum of interior angles
on the same side of transversal is 180°, then the lines are _______.
In the following figure, if OP || RS, ∠OPQ = 110° and ∠QRS = 130°, then ∠PQR is equal to ______.

In the following figure, find the value of x for which the lines l and m are parallel.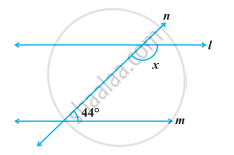
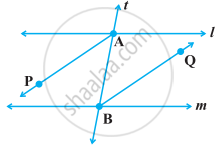
AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (Figure). Show that AP || BQ.
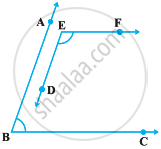
In the following figure, BA || ED and BC || EF. Show that ∠ABC + ∠DEF = 180°
A transversal intersects two parallel lines. Prove that the bisectors of any pair of corresponding angles so formed are parallel.
