Advertisements
Advertisements
प्रश्न
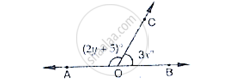
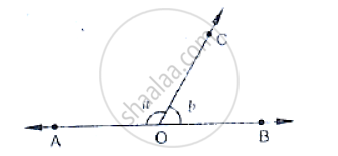
In the below Fig, OA and OB are opposite rays :
If x = 25°, what is the value of y?
उत्तर १
Given that x = 25°
Since `∠`AOC and `∠`BOC form a linear pair
`∠`AOC + `∠`BOC = 180°
Given that
`∠`AOC = 2 y + 5 and `∠`BOC = 3x
∴ `∠`AOC + `∠`BOC = 180°
(2 y + 5)° + 3x = 180°
(2 y + 5)° + 3(25°) = 180°
2 y° + 5° + 75° = 180°
2 y° + 80° = 180°
2 y° = 180° - 80° = 100°
y° = `(100°)/2` = 50°
⇒ y = 50°
उत्तर २
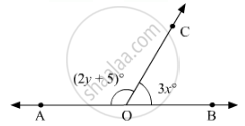
In figure:
Since OA and OB are opposite rays. Therefore, AB is a line. Since, OC stands on line AB.
Thus,∠AOCand ∠BOC form a linear pair, therefore, their sum must be equal to180°.
Or, we can say that
∠AOC + ∠BOC = 180°
From the given figure:
∠AOC= (2y + 5)and ∠BOC = 3x
On substituting these two values, we get
`(2y + 5) + 3x = 180`
`3x + 2y = 180 -5`
3x + 2y = 175 ...(i)
On putting x = 25in (i), we get:
`3(25 )+2y = 175`
`75 + 2y = 175`
`2y = 175 - 75`
`2y = 100`
`y = 100/2`
`y = 50`
Hence, the value of y is 50.
APPEARS IN
संबंधित प्रश्न
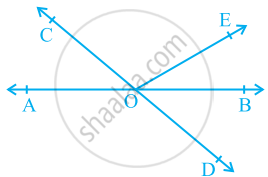
In the given figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD = 40°, find ∠BOE and reflex ∠COE.
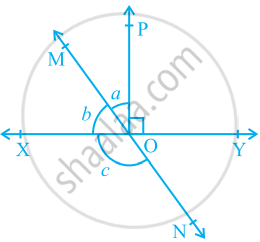
In the given figure, lines XY and MN intersect at O. If ∠POY = 90° and a : b = 2 : 3, find c.
Write the complement of the following angles .
30°
Two supplementary angles differ by 48°. Find the angles.
If an angle differs from its complement by 10°, find the angle .
In the below Fig, ∠AOC and ∠BOC form a linear pair. if a − 2b = 30°, find a and b.
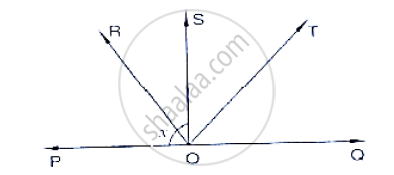
In below fig, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS
and ∠SOQ respectively. If ∠POS = x, find ∠ROT.
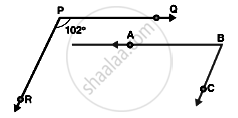
In the below, PQ || AB and PR || BC. If `∠`QPR = 102°, determine `∠`ABC. Give reasons.
Two unequal angles of a parallelogram are in the ratio 2 : 3. Find all its angles in degrees .
Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then each pair of corresponding
angles are _______
