Advertisements
Advertisements
Question
If below fig, ∠AOF and ∠FOG form a linear pair.
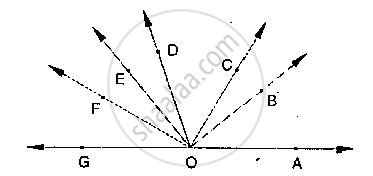
∠EOB = ∠FOC = 90° and ∠DOC = ∠FOG = ∠AOB = 30°
(i) Find the measures of ∠FOE, ∠COB and ∠DOE.
(ii) Name all the right angles.
(iii) Name three pairs of adjacent complementary angles.
(iv) Name three pairs of adjacent supplementary angles.
(v) Name three pairs of adjacent angles.
Solution
(i) `∠`FOE = x, `∠`DOE = y and `∠`BOC = z sat
Since `∠`AOF , `∠`FOG is Linear pair
⇒`∠`AOF + 30° = 180° [`∠`AOF + `∠`FOG = 180° and `∠`FOG = 30°]
⇒ `∠`AOF = 180° - 30°
⇒ `∠`AOF = 150°
⇒ `∠` AOB + `∠`BOC + `∠`COD + `∠`DOE + `∠`EOF = 150°
⇒ 30° + z + 30° + y + x = 150°
⇒ x + y + z = 150° - 30° - 30°
⇒ x + y + z = 90° .....(1)
Now `∠`FOC = 90°
⇒ `∠`FOE + `∠`EOD + `∠`DOC = 90°
⇒ x + y + 30° = 90°
⇒ x + y = 90° - 30°
⇒ x + y = 60° .....(2)
Substituting (2) in (1)
x + y + z = 90°
⇒ 60 + z = 90° Þ z = 90° - 60° = 30°
i.e., `∠`BOC = 30°
Given `∠`BOE = 90°
⇒`∠`BOC + `∠`COD + `∠`DOE = 90°
⇒ 30° + 30° + `∠`DOE = 90°
⇒ `∠`DOE = 90° - 60° = 30°
∴ `∠`DOE = x = 30°
Now, also we have
x + y = 60°
⇒ y = 60° - x = 60° - 30° = 30°
`∠`FOE = 30
(ii) Right angles are
`∠`DOG, `∠`COF , `∠`BOF , `∠`AOD
(iii) Three pairs of adjacent complementary angles are
`∠`AOB, `∠`BOD;
`∠`AOC, `∠`COD;
`∠`BOC, `∠`COE
(iv) Three pairs of adjacent supplementary angles are
`∠`AOB, `∠`BOG;
`∠`AOC, `∠`COG;
`∠`AOD, `∠`DOG.
(v) Three pairs of adjacent angles
`∠`BOC, `∠`COD;
`∠`COD, `∠`DOE;
`∠`DOE, `∠`EOF ,
APPEARS IN
RELATED QUESTIONS
Write the complement of the following angle.
20°
Write the complement of the following angles.
90°
Write the complement of the following angles .
30°
If an angle differs from its complement by 10°, find the angle .
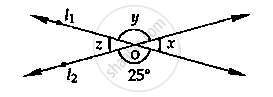
In the given fig, find the values of x, y and z.
In the below fig, find the value of x.

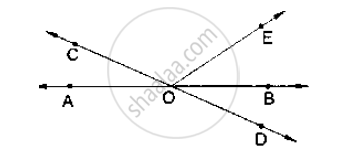
In below figure, lines AB and CD intersect at O. If ∠AOC + ∠BOE = 70° and ∠BOD =
40°, find ∠BOE and reflex ∠COE.
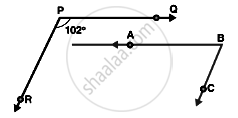
In the below, PQ || AB and PR || BC. If `∠`QPR = 102°, determine `∠`ABC. Give reasons.
Prove that if the two arms of an angle are perpendicular to the two arms of another angle, then the angles are either equal or supplementary
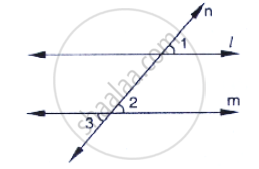
In the below fig, `∠`1 = 60° and `∠`2 = `(2/3)^(rd)`of a right angle. Prove that l || m.