Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Notes
Let the coordinates of a point be (3, 5). We want to plot this point in the coordinate plane. We draw the coordinate axes, and choose our units such that one centimetre represents one unit on both the axes. The coordinates of the point (3, 5) tell us that the distance of this point from the y - axis along the positive x - axis is 3 units and the distance of the point from the x - axis along the positive y - axis is 5 units. Starting from the origin O, we count 3 units on the positive x - axis and mark the corresponding point as A. Now, starting from A, we move in the positive direction of the y - axis and count 5 units and mark the corresponding point as P as the following fig.
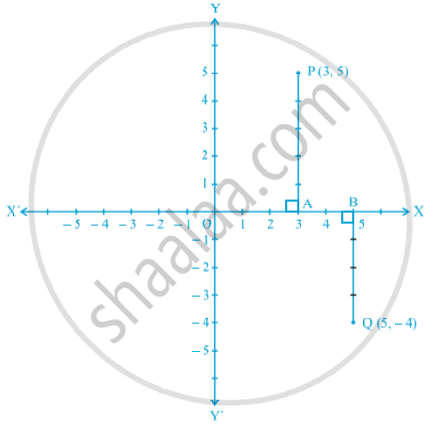
The distance of P from the y - axis is 3 units and from the x - axis is 5 units. Hence, P is the position of the point. Note that P lies in the 1st quadrant, since both the coordinates of P are positive. Similarly, you can plot the point Q (5, – 4) in the coordinate plane. The distance of Q from the x - axis is 4 units along the negative y - axis, so that its y - coordinate is – 4 as above fig. The point Q lies in the 4th quadrant.