Advertisements
Advertisements
प्रश्न
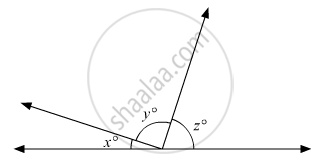
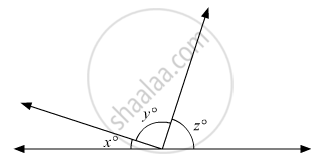
In the given figure, if \[\frac{y}{x} = 5\] and \[\frac{z}{x} = 4\] then the value of x isc
विकल्प
8°
18°
12°
15°
उत्तर
In the given figure, we havex°,y° and z° forming a linear pair, therefore these must be supplementary.
That is,
x + y +z = 180° (i)
Also,
`y/x = 5`
y = 5x (ii)
And
`z/x = 4`
z = 4x (iii)
Substituting (ii) and (iii) in (i), we get:
x + 5x + 4x = 180°
10x = 180°
`x = (180°)/10`
x = 18°
APPEARS IN
संबंधित प्रश्न
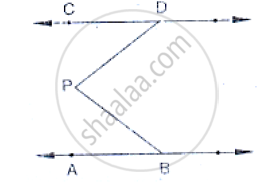
In the below fig, lines AB and CD are parallel and P is any point as shown in the figure.
Show that` ∠`ABP +` ∠`CDP = ∠DPB.
Prove that the straight lines perpendicular to the same straight line are parallel to one
another.
In the below fig, p is a transversal to lines m and n,`∠`2 = 120° and `a∠`5 = 60°. Prove that m || n.
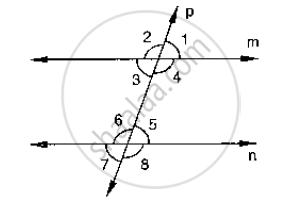
Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
Fill in the blank in the following to make the statement true:
If two parallel lines are intersected by a transversal, then interior angles on the same
side of the transversal are _______
Fill in the blank in the following to make the statement true:
If a transversal intersects a pair of lines in such a way that a pair of alternate angles
are equal, then the lines are _______
Fill in the blank :
If a transversal intersects a pair of lines in such a way that the sum of interior angles
on the same side of transversal is 180°, then the lines are _______.
In the following figure, find the value of x for which the lines l and m are parallel.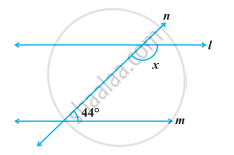
Two lines l and m are perpendicular to the same line n. Are l and m perpendicular to each other? Give reason for your answer.
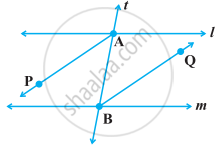
AP and BQ are the bisectors of the two alternate interior angles formed by the intersection of a transversal t with parallel lines l and m (Figure). Show that AP || BQ.