Advertisements
Advertisements
Question
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is ______.
Options
60°
40°
80°
20°
Solution
Angles of a triangle are in the ratio 2 : 4 : 3. The smallest angle of the triangle is 40°.
Explanation:
Given, the ratio of angles of a triangle is 2 : 4 : 3.
Let the angles of a triangle be ∠A, ∠B and ∠C.
∠A = 2x, ∠B = 4x and ∠C = 3x ,
∠A + ∠B + ∠C = 180° ...[Sum of all the angles of a triangle is 180°]
2x + 4x + 3x = 180°
9x = 180°
x =
∠A = 2x = 2 × 20° = 40°
∠B = 4x = 4 × 20° = 80°
∠C = 3x = 3 × 20° = 60°
Hence, the smallest angle of a triangle is 40°.
APPEARS IN
RELATED QUESTIONS
In the following triangle, find the value of x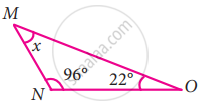
In the following triangle, find the value of x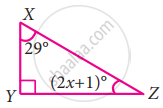
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S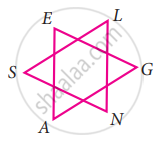
In ∆ABC, if ∠B is 3 times ∠A and ∠C is 2 times ∠A, then find the angle
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM =
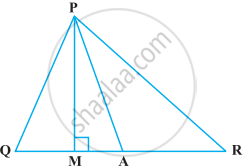
If one of the angles of a triangle is 110°, then the angle between the bisectors of the other two angles is ______.
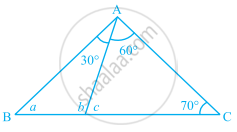
In the given figure, find the values of a, b and c.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
I have three sides. One of my angle measures 15°. Another has a measure of 60°. What kind of a polygon am I? If I am a triangle, then what kind of triangle am I?
The angles of a triangle are arranged in descending order of their magnitudes. If the difference between two consecutive angles is 10°, find the three angles.
