Advertisements
Advertisements
Question
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
Solution
Given ∠F = 48°
∠E = 68°
In ∆DEF,
∠D + ∠F + ∠E = 180° ...[By angle sum property]
∠D + 68° + 68° = 180°
∠D + 116° = 180°
∠D = 180° – 116°
= 64°
Since DG is the angular bisector of ∠D
∠FDG = ∠GDE
Also ∠FDG + ∠GDE = ∠D
2 ∠FDG = 64°
2 ∠FDG = 64°
∠FDG = `(64^circ)/2` = 32°
∠FDG = 32°
In ∆FDG,
∠FDG + ∠GFD = 180° ...[By angle sum property of triangles]
32° + ∠FDG + 48° = 180°
∠FDG + 80° = 180°
∠FDG = 180° – 80°
∠FDG = 100°
APPEARS IN
RELATED QUESTIONS
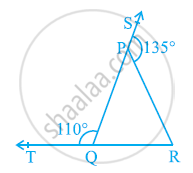
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
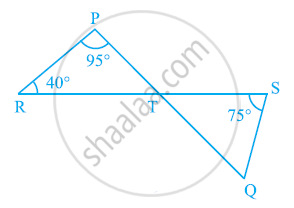
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
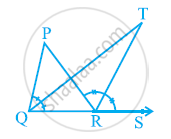
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
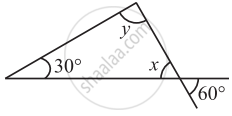
Find the value of the unknown x and y in the following diagram:
Observe the figure and find the value of ∠A + ∠N + ∠G + ∠L + ∠E + ∠S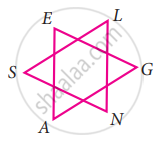
If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
It is possible to have a triangle in which two of the angles are right angles.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

