Advertisements
Advertisements
Question
In the figure find the value of x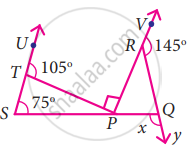
Solution
Exterior angle is equal to the sum of opposite interior angles.
In ∆TSP ∠TSP + ∠SPT = ∠UTP
75° + ∠SPT = 105°
∠SPT = 105° – 75°
∠SPT = 30° ...(1)
∠SPT + ∠TPR + ∠RPQ = 180° ...[∵ Sum of angles at a point on a line is 180°]
30° + 90° + ∠RPQ = 180°
120° + ∠RPQ = 180°
∠RPQ = 180° – 120°
∠RPQ = 60° ...(2)
∠VRQ + ∠QRP = 180° ...[∵ linear pair]
145° + ∠QRP = 180°
∠QRP = 180° – 145°
∠QRP = 35°
Now in ∆PQR
∠QRP + ∠RPQ = x ...[∵ x in the exterior angle]
35° + 60° = x
95° = x
APPEARS IN
RELATED QUESTIONS
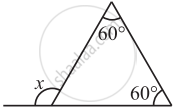
Find the value of the unknown exterior angle x in the following diagram:
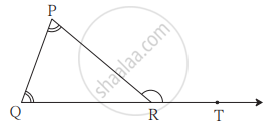
In ∆PQR, the measures of ∠P and ∠Q are equal and m∠PRQ = 70°. Find the measures of the following angles.
- m∠PRT
- m∠P
- m∠Q
If an exterior angle of a triangle is 115° and one of the interior opposite angles is 35°, then the other two angles of the triangle are
If the exterior angle of a triangle is 140° and its interior opposite angles are equal, find all the interior angles of the triangle
Find the value of ‘x’ in the given figure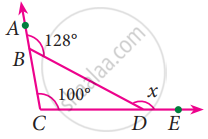
In the given figure BD = BC, find the value of x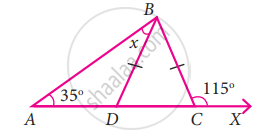
In the given figure find the value of x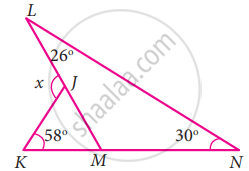
From the given figure find the value of y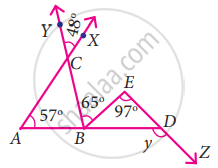
From the given figure, the value of x is ______.
In the given figure, ∠TPQ = ∠ _____ + ∠ _____