Advertisements
Advertisements
Question
In the given figure BD = BC, find the value of x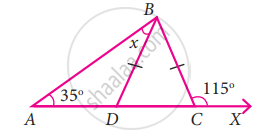
Solution
Given that BD = BC
∆BDC is on isosceles triangle.
In isosceles triangle, angles opposite to equal sides are equal.
∠BDC = ∠BCD ...(1)
Also ∠BCD + ∠BCX = 180° ...[∵ Liner Pair]
∠BCD + 115° = 180°
∠BCD = 180° – 115°
∠BCD = 65° ...[By (1)]
In ∆ADB
∠BAD + ∠ADB = ∠BDC ...[∵ BDC is the exterior angle and ∠BAD and ∠ABD are interior opposite angles]
35° + x = 65°
x = 65° – 35°
x = 30°
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown exterior angle x in the following diagram:
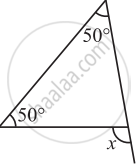
Find the value of the unknown interior angle x in the following figure.
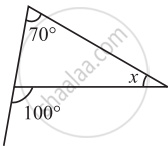
Find the value of the unknown interior angle x in the following figure.

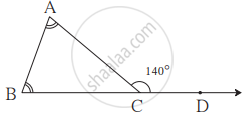
∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
In the isosceles triangle ABC, ∠A, and ∠B are equal. ∠ACD is an exterior angle of ∆ABC. The measures of ∠ACB and ∠ACD are (3x − 17)° and (8x + 10)°, respectively. Find the measures of ∠ACB and ∠ACD. Also find the measures of ∠A and ∠B.
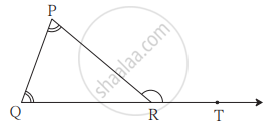
In ∆PQR, the measures of ∠P and ∠Q are equal and m∠PRQ = 70°. Find the measures of the following angles.
- m∠PRT
- m∠P
- m∠Q
In the given figure find the values of x and y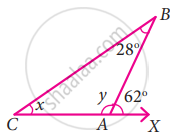
From the given figure find the value of y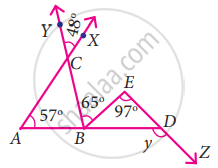
From the given figure, the value of x is ______.
In the given figure, ∠UQR = ∠______ + ∠ ______