Advertisements
Advertisements
Question
Using the given figure, prove that the triangles are congruent. Can you conclude that AC is parallel to DE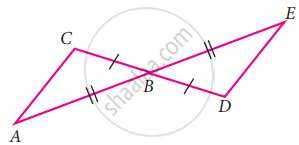
Solution
In ∆ABC and ∆EBD,
AB = EB
BC = BD
∠ABC = ∠EBD ...[∵ Vertically opposite angles]
By SAS congruency criteria ∆ABC ≅ ∆EBD.
We know that corresponding parts of congruent triangles are congruent.
∴ ∠BCA ≅ ∠BDE and ∠BAC ≅ ∠BED
∠BCA ≅ ∠BDE means that alternate interior angles are equal if CD is the transversal to lines AC and DE.
Similarly, if AE is the transversal to AC and DE,
we have ∠BAC ≅ ∠BED
Again interior opposite angles are equal.
We can conclude that AC is parallel to DE.
APPEARS IN
RELATED QUESTIONS
Given below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using the SAS congruence rule. If the triangles are congruent, write them in symbolic form.
∆ABC, AB = 7 cm, BC = 5 cm, ∠B = 50°.
∆DEF, DE = 5 cm, EF = 7 cm, ∠E = 50°.
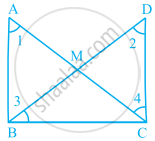
In the given figure, M is the mid-point of both AC and BD. Then ______.
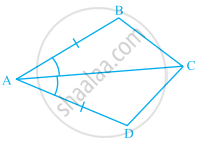
In the given figure, AB = AD and ∠BAC = ∠DAC. Then
- ∆ ______ ≅ ∆ABC.
- BC = ______.
- ∠BCA = ______.
- Line segment AC bisects ______ and ______.
In the given figures, two triangles are congruent by RHS.
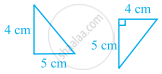
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
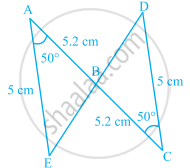
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
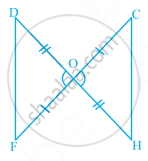
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.
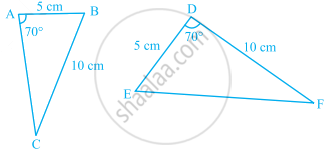
In the given figure, which pairs of triangles are congruent by SAS congruence criterion (condition)? if congruent, write the congruence of the two triangles in symbolic form.

State which of the following pairs of triangles are congruent. If yes, write them in symbolic form (you may draw a rough figure).
∆ABC: AB = 4.8 cm, ∠A = 90°, AC = 6.8 cm
∆XYZ: YZ = 6.8 cm, ∠X = 90°, ZX = 4.8 cm
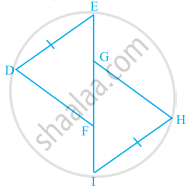
In the given figure, DE = IH, EG = FI and ∠E = ∠I. Is ∆DEF ≅ ∆HIG? If yes, by which congruence criterion?