Advertisements
Advertisements
Question
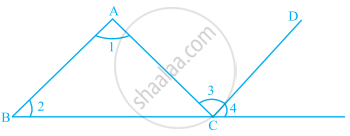
∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
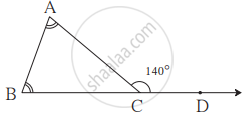
Solution
Let the measures of ∠A be x°.
m∠A = m∠B = x°
∠ACD is the exterior angle of ∆ABC
∴ m∠ACD = m∠A + m∠B
∴ 140° = x + x
∴ 140° = 2x
∴ 2x = 140°
∴ x = `140^circ/2`
= 70°
∴ The measures of the angles ∠A and ∠B are 70°, respectively.
RELATED QUESTIONS
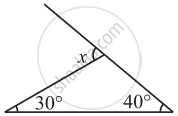
Find the value of the unknown exterior angle x in the following diagram:
Find the value of the unknown exterior angle x in the following diagram:
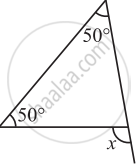
Find the value of the unknown interior angle x in the following figure.
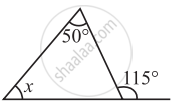
Find the value of the unknown interior angle x in the following figure.
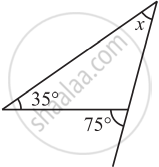
Find the value of x in the given triangle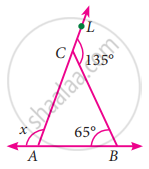
If the exterior angle of a triangle is 140° and its interior opposite angles are equal, find all the interior angles of the triangle
In the figure find the value of x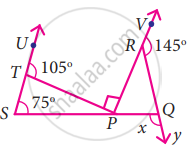
In the given figure, the value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F is ______.
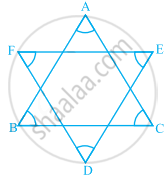
In the given figure, if AB || CD, then ______.
In the given figure, ∆PQR is right-angled at P. U and T are the points on line QRF. If OP || ST and US || RP, find ∠S.

