Advertisements
Advertisements
Question
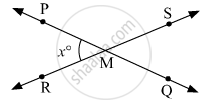
Lines PQ and RS intersect at point M. m∠PMR = x° What are the measures of ∠PMS, ∠SMQ and ∠QMR?
Solution
In the given figure,
∠RMP + ∠PMS = 180∘ (Linear Pair angles)
⇒ x∘ + ∠PMS = 180∘
⇒ ∠PMS = (180 − x)∘
Now,
∠PMR = ∠SMQ = x∘ (Vertically opposite angles)
∠PMS = ∠RMQ = (180 − x)∘ (Vertically opposite angles)
Hence, the measures of ∠PMS, ∠SMQ and ∠QMR are (180 − x)∘, x∘ and (180 − x)∘ respectively.
RELATED QUESTIONS
Fill in the blanks:
If two lines intersect at a point, and if one pair of vertically opposite angles are acute angles, then the other pair of vertically opposite angles are _______.
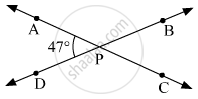
Lines AC and BD intersect at point P. m∠APD = 47°. Find the measures of ∠APB, ∠BPC, ∠CPD.
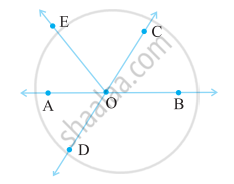
In the given figure, Identify two pairs of vertically opposite angles.
The angles at a point are x°, 2x°, 3x°, 4x° and 5x°. Find the value of the largest angle?
From the given figure, find the missing angle
In the figure AB is parallel to CD. Find x, y and z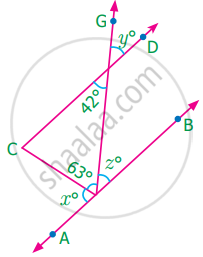
In the given figure, ∠8 = 107°, what is the sum of the ∠2 and ∠4?
Vertically opposite angles are always ______.
The sum of two vertically opposite angles is 166°. Find each of the angles.
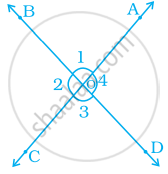
If two angles have a common vertex and their arms form opposite rays (Figure), Then, write all the pairs of vertically opposite angles.