Advertisements
Advertisements
प्रश्न
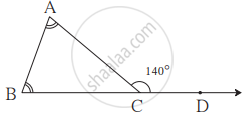
∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
उत्तर
Let the measures of ∠A be x°.
m∠A = m∠B = x°
∠ACD is the exterior angle of ∆ABC
∴ m∠ACD = m∠A + m∠B
∴ 140° = x + x
∴ 140° = 2x
∴ 2x = 140°
∴ x = `140^circ/2`
= 70°
∴ The measures of the angles ∠A and ∠B are 70°, respectively.
संबंधित प्रश्न
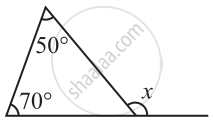
Find the value of the unknown exterior angle x in the following diagram:
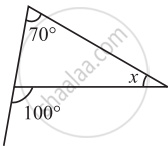
Find the value of the unknown interior angle x in the following figure.
If an exterior angle of a triangle is 115° and one of the interior opposite angles is 35°, then the other two angles of the triangle are
In the given figure find the value of x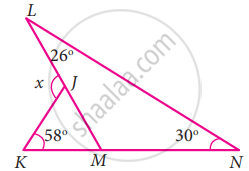
In the given figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to ______.
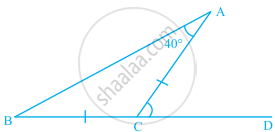
From the given figure, the value of x is ______.
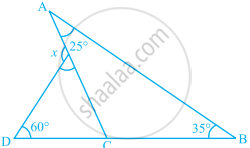
The measures of ∠x and ∠y in the given figure are respectively.
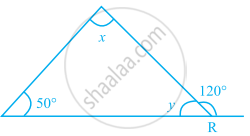
In the given figure, if AB || CD, then ______.
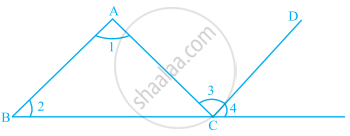
In the given figure, ∠UQR = ∠______ + ∠ ______
In ∆ABC, if ∠A = ∠C, and exterior angle ABX = 140°, then find the angles of the triangle.
