Advertisements
Advertisements
Question
From the given figure find the value of y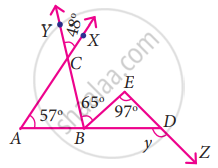
Solution
From the figure,
∠ACB = ∠XCY ...[Vertically opposite angles]
ACB = 48° ...(1)
In ∆ABC, ∠CBD is the exterior angle at B
Exterior angle = Sum of interior opposite angles
∠CBD = ∠BAC + ∠ACB
∠CBE + ∠EBD = 57° + 48°
65° + ∠EBD = 105°
∠EBD = 105° + 65° = 40° ...(2)
In ∆EBD, y is the exterior angle at D.
y = ∠EBD + ∠BED ...[∵ Exterior angle = Sum of opposite interior angles]
y = 40° + 97° ...[∵ From (2)]
y = 137°
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown exterior angle x in the following diagram:
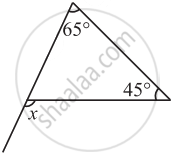
Find the value of the unknown interior angle x in the following figure.

Find the value of x in the given triangle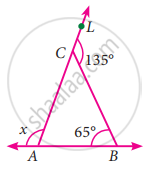
If an exterior angle of a triangle is 115° and one of the interior opposite angles is 35°, then the other two angles of the triangle are
In the given figure BD = BC, find the value of x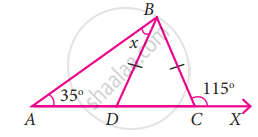
In the given figure find the values of x and y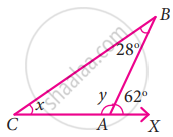
In the figure find the value of x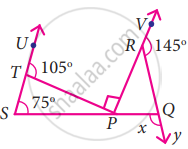
If the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is 360°.
In ∆ABC, if ∠A = ∠C, and exterior angle ABX = 140°, then find the angles of the triangle.
In the given figure, ∆PQR is right-angled at P. U and T are the points on line QRF. If OP || ST and US || RP, find ∠S.

