Advertisements
Advertisements
प्रश्न
From the given figure find the value of y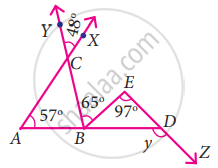
उत्तर
From the figure,
∠ACB = ∠XCY ...[Vertically opposite angles]
ACB = 48° ...(1)
In ∆ABC, ∠CBD is the exterior angle at B
Exterior angle = Sum of interior opposite angles
∠CBD = ∠BAC + ∠ACB
∠CBE + ∠EBD = 57° + 48°
65° + ∠EBD = 105°
∠EBD = 105° + 65° = 40° ...(2)
In ∆EBD, y is the exterior angle at D.
y = ∠EBD + ∠BED ...[∵ Exterior angle = Sum of opposite interior angles]
y = 40° + 97° ...[∵ From (2)]
y = 137°
APPEARS IN
संबंधित प्रश्न
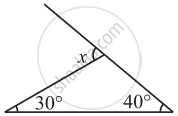
Find the value of the unknown exterior angle x in the following diagram:
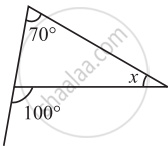
Find the value of the unknown interior angle x in the following figure.
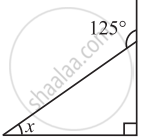
Find the value of the unknown interior angle x in the following figure.
Find the value of the unknown interior angle x in the following figure.

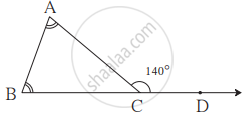
∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
Using the measures of the angles given in the figure alongside, find the measures of the remaining three angles.

Using the given figure find the value of x.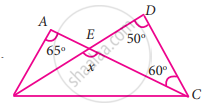
Find the value of x in the given triangle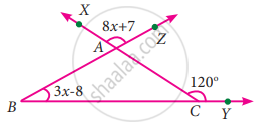
In the figure find the value of x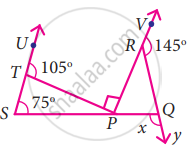
Find the value of x in the given figure.

