Advertisements
Advertisements
प्रश्न
Find the value of x in the given triangle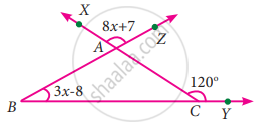
Advertisements
उत्तर
In ∆ABC, given B = 3x – 8°
∠XAZ = ∠BAC ...[∵ vertically opposite angles]
8x + 7 + ∠BAC
i.e., In ∆ABC, ∠A = 8x + 7
Exterior angle ∠XCY = 120°
Exterior angle is equal to the sum of the interior opposite angles
∠A + ∠B = 120°
8x + 7 + 3x – 8 = 120°
8x + 3x = 120° + 8 – 7
11x = 121°
x = `(121^circ)/11`
x = 11°
APPEARS IN
संबंधित प्रश्न
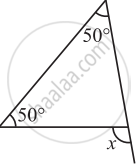
Find the value of the unknown exterior angle x in the following diagram:
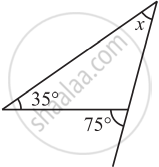
Find the value of the unknown interior angle x in the following figure.
Using the measures of the angles given in the figure alongside, find the measures of the remaining three angles.
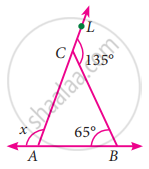
In ∆LMN, MN is extended to O. If ∠MLN = 100 – x, ∠LMN = 2x and ∠LNO = 6x – 5, find the value of x
An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
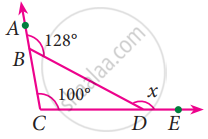
From the given figure find the value of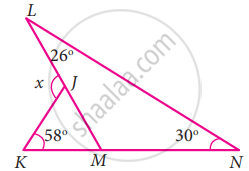 y
In the following figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to ______.
From the given figure, the value of x is ______.
If the exterior angle of a triangle is 130° and its interior opposite angles are equal, then measure of each interior opposite angle is ______.
In the following figure, if AB || CD, then ______.
