Advertisements
Advertisements
Question
Find the value of x in the given triangle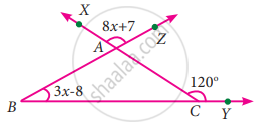
Solution
In ∆ABC, given B = 3x – 8°
∠XAZ = ∠BAC ...[∵ vertically opposite angles]
8x + 7 + ∠BAC
i.e., In ∆ABC, ∠A = 8x + 7
Exterior angle ∠XCY = 120°
Exterior angle is equal to the sum of the interior opposite angles
∠A + ∠B = 120°
8x + 7 + 3x – 8 = 120°
8x + 3x = 120° + 8 – 7
11x = 121°
x = `(121^circ)/11`
x = 11°
APPEARS IN
RELATED QUESTIONS
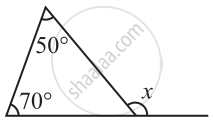
Find the value of the unknown exterior angle x in the following diagram:
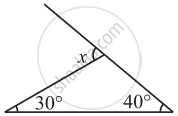
Find the value of the unknown exterior angle x in the following diagram:
In the isosceles triangle ABC, ∠A, and ∠B are equal. ∠ACD is an exterior angle of ∆ABC. The measures of ∠ACB and ∠ACD are (3x − 17)° and (8x + 10)°, respectively. Find the measures of ∠ACB and ∠ACD. Also find the measures of ∠A and ∠B.
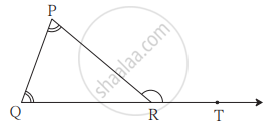
In ∆PQR, the measures of ∠P and ∠Q are equal and m∠PRQ = 70°. Find the measures of the following angles.
- m∠PRT
- m∠P
- m∠Q
An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
Find the value of ‘x’ in the given figure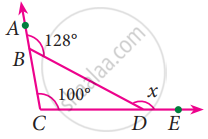
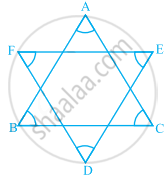
In the given figure, the value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F is ______.
Which of the following triplets cannot be the angles of a triangle?
In ∆ABC, ∠Α = 50°, ∠B = 70° and bisector of ∠C meets AB in D (see figure). Measure of ∠ADC is ______.
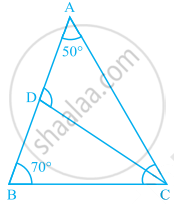
In the given figure, ∠PRS = ∠ ______ + ∠ _______