Advertisements
Advertisements
Question
Which of the following triplets cannot be the angles of a triangle?
Options
67°, 51°, 62°
70°, 83°, 27°
90°, 70°, 20°
40°, 132°, 18°
Solution
40°, 132°, 18°
Explanation:
We know that, the sum of the interior angles of a triangle is 180°.
Now, we will verify the given triplets:
- 67° + 51° + 62° = 180°
- 70° + 83° + 27° = 180°
- 90° + 70° + 20° = 180°
- 40° + 132° + 18° = 190°
APPEARS IN
RELATED QUESTIONS
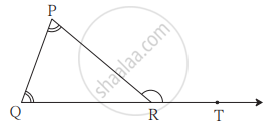
In ∆PQR, the measures of ∠P and ∠Q are equal and m∠PRQ = 70°. Find the measures of the following angles.
- m∠PRT
- m∠P
- m∠Q
Using the given figure find the value of x.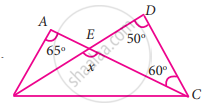
Using the diagram find the value of x.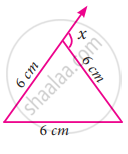
If the exterior angle of a triangle is 140° and its interior opposite angles are equal, find all the interior angles of the triangle
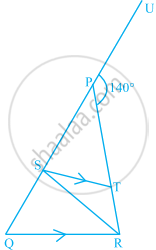
In the given figure, PQ = PR, RS = RQ and ST || QR. If the exterior angle RPU is 140°, then the measure of angle TSR is ______.
In the given figure, ∠TPQ = ∠ _____ + ∠ _____
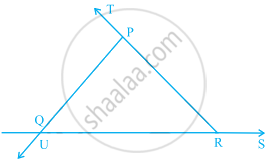
In the given figure, ∠UQR = ∠______ + ∠ ______
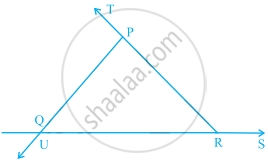
In the given figure, ∠PRS = ∠ ______ + ∠ _______
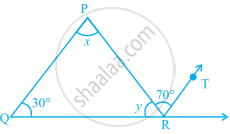
In the given figure QP || RT. Find the values of x and y.
In ∆ABC, if ∠A = ∠C, and exterior angle ABX = 140°, then find the angles of the triangle.
