Advertisements
Advertisements
Question
In ∆ABC, if ∠A = ∠C, and exterior angle ABX = 140°, then find the angles of the triangle.
Solution
Given, ∠A = ∠C and exterior ∠ABX = 140°
Let ∠A = ∠C = x
According to the exterior angle property,

Exterior ∠B = Interior ∠A + Interior ∠C
⇒ 140° = x + x
⇒ 140° = 2x
⇒ x = `140^circ/2` = 70°
So, ∠A = ∠C = 70°
Now, ∠A + ∠B + ∠C = 180° ......[Angle sum property of a triangle]
⇒ 70 + ∠B + 70° = 180°
⇒ ∠B + 140° = 180°
⇒ ∠B = 180° – 140°
⇒ ∠B = 40°
Hence, all the angles of the triangles are 70°, 40° and 70°.
APPEARS IN
RELATED QUESTIONS
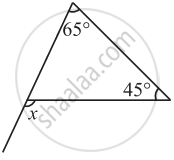
Find the value of the unknown exterior angle x in the following diagram:
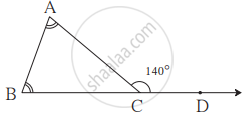
∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
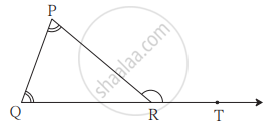
In ∆PQR, the measures of ∠P and ∠Q are equal and m∠PRQ = 70°. Find the measures of the following angles.
- m∠PRT
- m∠P
- m∠Q
Find the value of x in the given triangle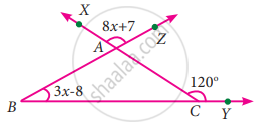
Find the value of ‘x’ in the given figure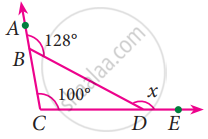
In the given figure find the values of x and y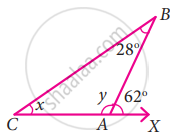
From the given figure, the value of x is ______.
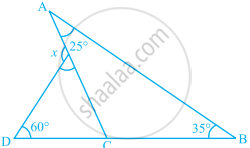
The measures of ∠x and ∠y in the given figure are respectively.
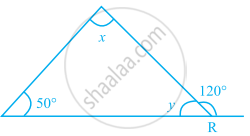
If the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is 360°.
Find the value of x in the given figure.

