Advertisements
Advertisements
Question
Find the value of x in the given figure.

Solution
In the given figure, ∠BAC = 80°, ∠ABC = 30°, ∠ACE = x and ∠ECD = 90°
In ΔABC, we know that, exterior angle is equal to the sum of interior opposite angles.
∴ ∠ACD = ∠CAB + ∠ABC
⇒ ∠ACE + ∠ECD = 80° + 30° ......[∵ ∠ACD = ∠ACE + ∠ECD]
⇒ ∠ACE + 90° = 110° ......[∵ ∠ECD = 90°]
⇒ ∠ACE = 110° – 90° = 20°
APPEARS IN
RELATED QUESTIONS
Using the measures of the angles given in the figure alongside, find the measures of the remaining three angles.

Find the value of x in the given triangle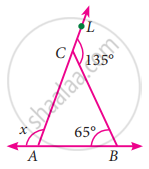
An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
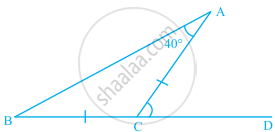
In the given figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to ______.
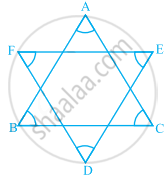
In the given figure, the value of ∠A + ∠B + ∠C + ∠D + ∠E + ∠F is ______.
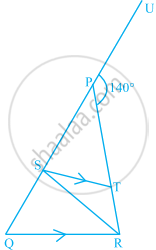
In the given figure, PQ = PR, RS = RQ and ST || QR. If the exterior angle RPU is 140°, then the measure of angle TSR is ______.
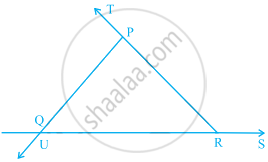
In ∆PQR, if ∠P = 60°, and ∠Q = 40°, then the exterior angle formed by producing QR is equal to ______.
In the given figure, ∠PRS = ∠ ______ + ∠ _______
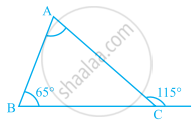
Find the measure of ∠A in the given figure.
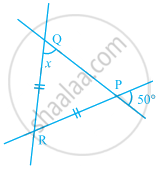
In the given figure, if RP = RQ, find the value of x.