Advertisements
Advertisements
Question
In ∆LMN, MN is extended to O. If ∠MLN = 100 – x, ∠LMN = 2x and ∠LNO = 6x – 5, find the value of x
Solution
Exterior angle is equal to the sum of the opposite interior angles
∠LNO = ∠MLN + ∠LMN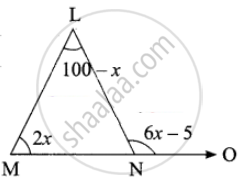
6x – 5 = 100° – x + 2x
6x – 5 + x – 2x = 100°
6x + x – 2x = 100° + 5°
5x = 105°
x = `(105^circ)/5` = 21°
x = 21°
APPEARS IN
RELATED QUESTIONS
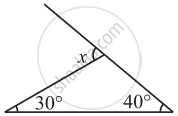
Find the value of the unknown exterior angle x in the following diagram:
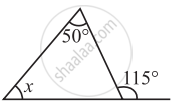
Find the value of the unknown interior angle x in the following figure.
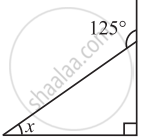
Find the value of the unknown interior angle x in the following figure.
Find the value of the unknown interior angle x in the following figure.

Find the value of the unknown interior angle x in the following figure.
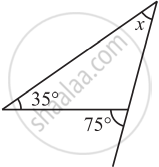
Find angle x in Fig

An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
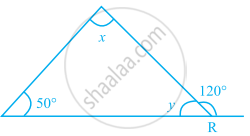
The measures of ∠x and ∠y in the given figure are respectively.
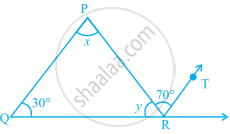
In the given figure QP || RT. Find the values of x and y.
If the sides of a triangle are produced in an order, show that the sum of the exterior angles so formed is 360°.
