Advertisements
Advertisements
Question
In the isosceles triangle ABC, ∠A, and ∠B are equal. ∠ACD is an exterior angle of ∆ABC. The measures of ∠ACB and ∠ACD are (3x − 17)° and (8x + 10)°, respectively. Find the measures of ∠ACB and ∠ACD. Also find the measures of ∠A and ∠B.
Solution
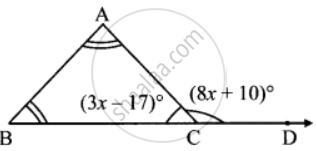
Given:
∠ACB = (3x − 17)∘
∠ACD = (8x + 10)∘
Now, ∠ACB + ∠ACD = 180∘ ...(Linear Pair angles)
⇒ 3x° − 17° + 8x° + 10° = 180°
⇒ 3x° + 8x° − 17° + 10° = 180°
⇒ 11x° − 7° = 180°
⇒ 11x° – 7° + 7° = 180° + 7 ...(Adding 7 on both sides.)
⇒ 11x° = 187°
⇒ x° = `187°/11°`
⇒ x° = 17°
Therefore,
∠ACB = (3x − 17)°
= (3 × 17)° − 17°
= (51 − 17)°
= 34°
∠ACD = (8x + 10)°
= (8 × 17)° + 10°
= (136 + 10)°
= 146°
Now, ∠A + ∠B = ∠ACD ...(Exterior angle property)
⇒ 2∠A = 146° (∵∠A = ∠B)
⇒ ∠A = `146°/2`
⇒ ∠A = 73°
Hence, the measures of ∠ACB, ∠ACD, ∠A and ∠B are 146°, 34°, 73° and 73°, respectively.
RELATED QUESTIONS
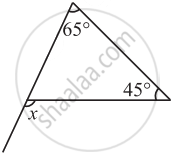
Find the value of the unknown exterior angle x in the following diagram:
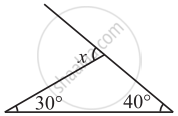
Find the value of the unknown exterior angle x in the following diagram:
Find the value of the unknown interior angle x in the following figure.
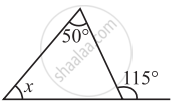
Find the value of the unknown interior angle x in the following figure.

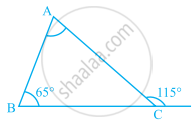
Find angle x in Fig

Find the value of x in the given triangle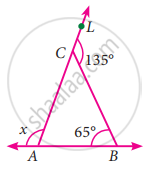
Find the value of x in the given triangle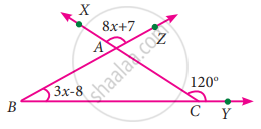
An exterior angle of a triangle is 70° and two interior opposite angles are equal. Then measure of each of these angle will be
Which of the following triplets cannot be the angles of a triangle?
Find the measure of ∠A in the given figure.