Advertisements
Advertisements
प्रश्न
Find the value of ‘x’ in the given figure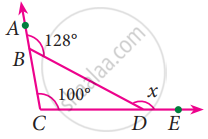
उत्तर
Given ∠DCB = 100° and ∠DBA = 128°
In the given figure
∠CBD + ∠DBA = 180°
∠CBD + 128° = 180°
∠CBD = 52°
Now exterior angle x = Sum of interior opposite angles.
x = ∠DCB + ∠CBD
= 100° + 52°
= 152°
x = 152°
APPEARS IN
संबंधित प्रश्न
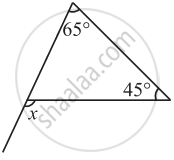
Find the value of the unknown exterior angle x in the following diagram:
Find the value of the unknown exterior angle x in the following diagram:
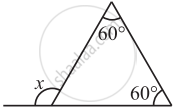
Find the value of the unknown exterior angle x in the following diagram:
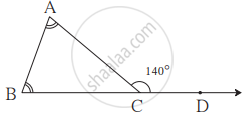
∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
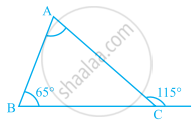
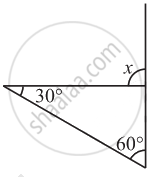
Find angle x in Fig

In the given figure BD = BC, find the value of x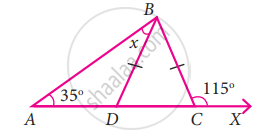
If the exterior angle of a triangle is 130° and its interior opposite angles are equal, then measure of each interior opposite angle is ______.
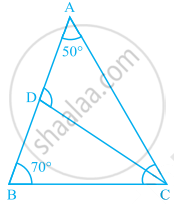
In ∆ABC, ∠Α = 50°, ∠B = 70° and bisector of ∠C meets AB in D (see figure). Measure of ∠ADC is ______.
In the given figure QP || RT. Find the values of x and y.
Find the measure of ∠A in the given figure.