Advertisements
Advertisements
प्रश्न
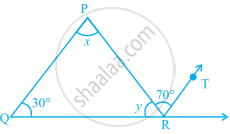
In the given figure QP || RT. Find the values of x and y.
उत्तर
QP || RT and PR is a transversal.
∴ ∠QPR = ∠PRT ......[Alternate interior angles]
⇒ x = 70°
Now, OP || RT and OR is a transversal.
∴ ∠PQR + ∠QRT = 180° ......[Co-interior angles]
⇒ 30° + y + 70° = 180°
⇒ y = 180° – 30° – 70° = 80°
Thus, x = 70° and y = 80°
APPEARS IN
संबंधित प्रश्न
Find the value of the unknown exterior angle x in the following diagram:
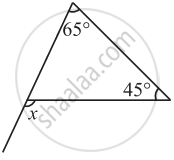
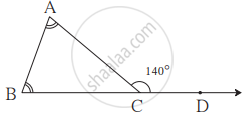
∠ACD is an exterior angle of ∆ABC. The measures of ∠A and ∠B are equal. If m∠ACD = 140°, find the measures of the angles ∠A and ∠B.
Find angle x in Fig

In ∆LMN, MN is extended to O. If ∠MLN = 100 – x, ∠LMN = 2x and ∠LNO = 6x – 5, find the value of x
In ∆JKL, if ∠J = 60° and ∠K = 40°, then find the value of exterior angle formed by extending the side KL
In the given figure find the values of x and y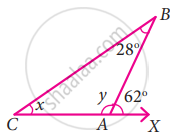
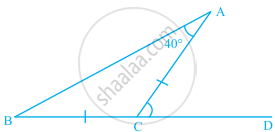
In the given figure, BC = CA and ∠A = 40°. Then, ∠ACD is equal to ______.
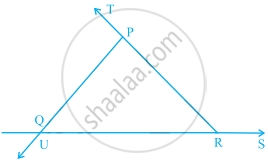
In the given figure, ∠UQR = ∠______ + ∠ ______
In ∆ABC, if ∠A = ∠C, and exterior angle ABX = 140°, then find the angles of the triangle.
In the given figure, ∆PQR is right-angled at P. U and T are the points on line QRF. If OP || ST and US || RP, find ∠S.

