Advertisements
Advertisements
Question
In ∆ABC, DE || BC (see figure). Find the values of x, y and z.

Solution
DE || BC and AB is a transversal.
∴ ∠ADE = ∠DBC .....[Corresponding angles]
⇒ x = 30°
Now, DE || BC and AC is a transversal.
∴ ∠AED = ∠ECB .....[Corresponding angles]
⇒ y = 40°
In ∆ABC,
∠A + ∠B + ∠C = 180° ......[Angle sum property]
⇒ z + 30° + 40° = 180°
⇒ z = 180° – 40° – 30° = 110°
Thus, x = 30°, y = 40° and z = 110°.
APPEARS IN
RELATED QUESTIONS
Find the value of the unknown x in the following diagram:
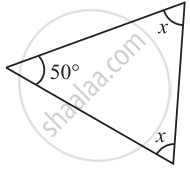
Find the value of the unknown x and y in the following diagram:
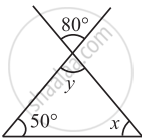
In the following triangle, find the value of x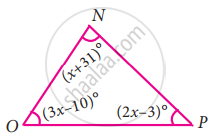
How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
If two angles of a triangle are 60° each, then the triangle is ______.
In the given figure, find the value of x.
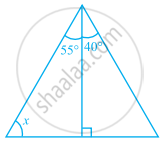
In a right-angled triangle if an angle measures 35°, then find the measure of the third angle.
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
In the given figure, if ST = SU, then find the values of x and y.

