Advertisements
Advertisements
Question
In ΔPQR, if 3∠P = 4∠Q = 6∠R, calculate the angles of the triangle.
Solution
Given, 3∠P = 4∠Q = 6∠R
Then, ∠P =
∠Q =
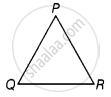
In ΔPQR, ∠P + ∠Q + ∠R = 180° .....[Angle sum property of a triangle]
⇒ 2∠R +
⇒ 3∠R +
⇒ 6∠R + 3∠R = 180° × 2 ......[On taking LCM in LHS]
⇒ 9∠R = 360°
⇒ ∠R =
∴ ∠P = 2∠R = 2 × 40° = 80°
And ∠Q =
Hence, all the angles of the triangle are 80°, 60° and 40°.
APPEARS IN
RELATED QUESTIONS
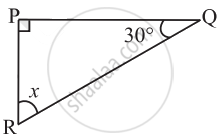
Find the value of the unknown x in the following diagram:
In the following triangle, find the value of x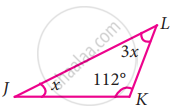
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
In the given figure, which of the following statement is true?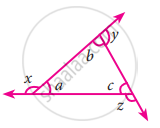
The angles of a triangle are in the ratio 2 : 3 : 4. Find the angles of the triangle.
The sum of the measures of three angles of a triangle is greater than 180°.
If two triangles are congruent, then the corresponding angles are equal.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
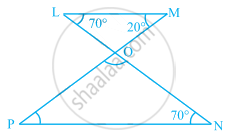
In the given figure, find the measures of ∠PON and ∠NPO.
If one angle of a triangle is 60° and the other two angles are in the ratio 1:2, find the angles.
