Advertisements
Advertisements
Question
If one angle of a triangle is 60° and the other two angles are in the ratio 1:2, find the angles.
Solution
Given, one angle of a triangle is 60°.
Let the other two angles be x and 2x.
We know that, the sum of all angles in a triangle is equal to 180°.
So, x + 2x + 60° = 180°
⇒ 3x = 180° – 60°
⇒ 3x = 120°
⇒ x = 40°
So, the other two angles will be x = 40° and 2x = 2 × 40° = 80°.
APPEARS IN
RELATED QUESTIONS
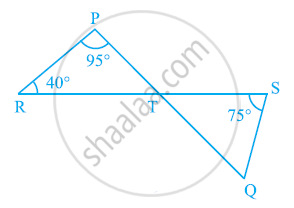
In the given figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40º, ∠RPT = 95º and ∠TSQ = 75º, find ∠SQT.
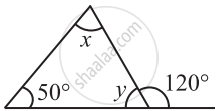
Find the value of the unknown x and y in the following diagram:
In the following triangle, find the value of x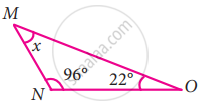
In the following triangle, find the value of x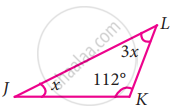
If the three angles of a triangle are in the ratio 3 : 5 : 4, then find them
Can a triangle have two obtuse angles? Give reason for your answer.
In a right-angled triangle, the angles other than the right angle are ______.
In the given figure, ∠BAC = 90°, AD ⊥ BC and ∠BAD = 50°, then ∠ACD is ______.

If one angle of a triangle is equal to the sum of the other two angles, the triangle is ______.
In the given figure, if ST = SU, then find the values of x and y.

