Advertisements
Advertisements
प्रश्न
If one angle of a triangle is 60° and the other two angles are in the ratio 1:2, find the angles.
उत्तर
Given, one angle of a triangle is 60°.
Let the other two angles be x and 2x.
We know that, the sum of all angles in a triangle is equal to 180°.
So, x + 2x + 60° = 180°
⇒ 3x = 180° – 60°
⇒ 3x = 120°
⇒ x = 40°
So, the other two angles will be x = 40° and 2x = 2 × 40° = 80°.
APPEARS IN
संबंधित प्रश्न
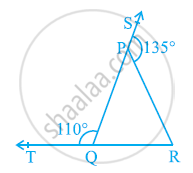
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
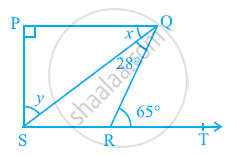
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
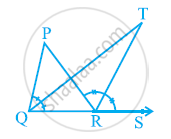
In the given figure, the side QR of ΔPQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR = 1/2∠QPR.
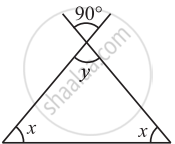
Find the value of the unknown x and y in the following diagram:
In the following triangle, find the value of x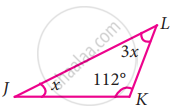
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
If one angle of a triangle is equal to the sum of other two, then the measure of that angle is ______.
It is possible to have a triangle in which two of the angles are right angles.
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
