Advertisements
Advertisements
प्रश्न
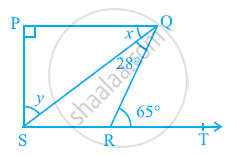
In the given figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28º and ∠QRT = 65º, then find the values of x and y.
उत्तर
It is given that PQ || SR and QR is a transversal line.
∠PQR = ∠QRT (Alternate interior angles)
x + 28º = 65º
x = 65º − 28º
x = 37º
By using the angle sum property for ΔSPQ, we obtain
∠SPQ + x + y = 180º
90º + 37º + y = 180º
y = 180º − 127º
y = 53º
∴x = 37º and y = 53º
APPEARS IN
संबंधित प्रश्न
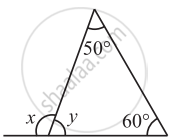
Find the value of the unknowns x and y in the following diagram:
In the following triangle, find the value of x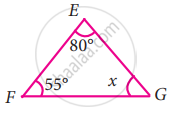
In the following triangle, find the value of x
Two line segments `bar("AD")` and `bar("BC")` intersect at O. Joining `bar("AB")` and `bar("DC")` we get two triangles, ∆AOB and ∆DOC as shown in the figure. Find the ∠A and ∠B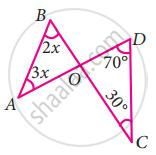
In ∆RST, ∠S is 10° greater than ∠R and ∠T is 5° less than ∠S, find the three angles of the triangle
The angles of a triangle are in the ratio 5 : 3 : 7. The triangle is ______.
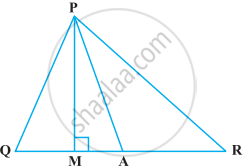
In the following figure, ∠Q > ∠R, PA is the bisector of ∠QPR and PM ⊥ QR. Prove that ∠APM = `1/2` (∠Q – ∠R).
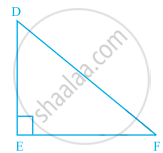
Triangle DEF of the given figure is a right triangle with ∠E = 90°. What type of angles are ∠D and ∠F?
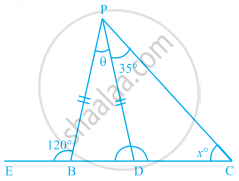
In the given figure, PB = PD. The value of x is ______.
If two triangles are congruent, then the corresponding angles are equal.
