Advertisements
Advertisements
Question
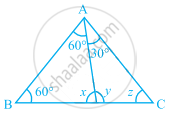
In the given figure, find the values of x, y and z.
Solution

In the give figure, ∠BAD = 60°, ∠ABD = 60°, ∠ADB = x, ∠DAC = 30°, ∠ADC = y and ∠ACD = z
We know that, the sum of all angles in a triangle is equal to 180°
In ΔABD, ∠BAD + ∠ABD + ∠ADB = 180°
⇒ 60° + 60° + x = 180°
⇒ 120° + x = 180°
⇒ x = 180° – 120°
⇒ x = 60°
Now, y = ∠BAD + ∠ABD ......[∵ Exterior angle is equal to the sum of interior opposite angles]
⇒ y = 60° + 60°
∴ y = 120°
In ΔADC, ∠DAC + ∠ADC + ∠ACD = 180° ......[Angle sum property of a triangle]
⇒ 30° + 120° + z = 180°
⇒ 150° + z = 180°
⇒ z = 180° – 150°
⇒ z = 30°
Hence, x = 60°, y = 120° and z = 30°.
APPEARS IN
RELATED QUESTIONS
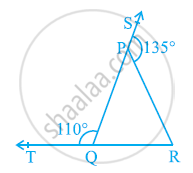
In the given figure, sides QP and RQ of ΔPQR are produced to points S and T respectively. If ∠SPR = 135º and ∠PQT = 110º, find ∠PRQ.
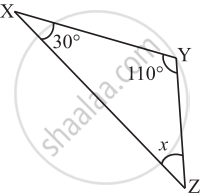
Find the value of the unknown x in the given diagram:
In a right angled triangle MNO, ∠N = 90°, MO is extended to P. If ∠NOP = 128°, find the other two angles of ∆MNO
Two adjacent angles are equal. Is it necessary that each of these angles will be a right angle? Justify your answer.
Prove that a triangle must have atleast two acute angles.
The sum of the measures of three angles of a triangle is greater than 180°.
The measure of three angles of a triangle are in the ratio 5:3:1. Find the measures of these angles.
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of ∠Y.
In the given figure, find the measures of ∠PON and ∠NPO.
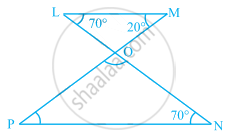
In the given figure, if ST = SU, then find the values of x and y.

