Advertisements
Advertisements
प्रश्न
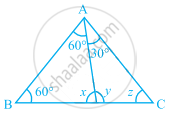
In the given figure, find the values of x, y and z.
उत्तर

In the give figure, ∠BAD = 60°, ∠ABD = 60°, ∠ADB = x, ∠DAC = 30°, ∠ADC = y and ∠ACD = z
We know that, the sum of all angles in a triangle is equal to 180°
In ΔABD, ∠BAD + ∠ABD + ∠ADB = 180°
⇒ 60° + 60° + x = 180°
⇒ 120° + x = 180°
⇒ x = 180° – 120°
⇒ x = 60°
Now, y = ∠BAD + ∠ABD ......[∵ Exterior angle is equal to the sum of interior opposite angles]
⇒ y = 60° + 60°
∴ y = 120°
In ΔADC, ∠DAC + ∠ADC + ∠ACD = 180° ......[Angle sum property of a triangle]
⇒ 30° + 120° + z = 180°
⇒ 150° + z = 180°
⇒ z = 180° – 150°
⇒ z = 30°
Hence, x = 60°, y = 120° and z = 30°.
APPEARS IN
संबंधित प्रश्न
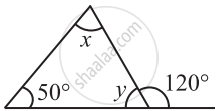
Find the value of the unknown x and y in the following diagram:
In the following triangle, find the value of x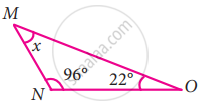
In the following triangle, find the value of x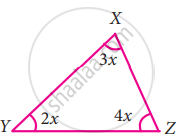
In ∆DEF, ∠F = 48°, ∠E = 68° and bisector of ∠D meets FE at G. Find ∠FGD
In an isosceles triangle, one angle is 70°. The other two angles are of ______.
- 55° and 55°
- 70° and 40°
- any measure
In the given option(s) which of the above statement(s) are true?
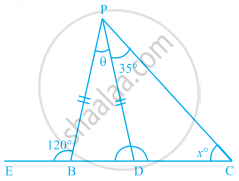
In the given figure, PB = PD. The value of x is ______.
By which of the following criterion two triangles cannot be proved congruent?
It is possible to have a triangle in which each angle is less than 60°.
In ΔDEF, ∠D = 60°, ∠E = 70° and the bisectors of ∠E and ∠F meet at O. Find (i) ∠F (i) ∠EOF.
In the given figure, if ST = SU, then find the values of x and y.

